Definizioni iniziali
Lunghezza di una stringa
La lunghezza di una stringa è il numero di simboli contenuti in una stringa (anche detta cardinalità e si indica con |x|).
La stringa vuota è la stringa che ha zero elementi (|\varepsilon| = 0).
Due stringhe sono uguali se e solo se:
- |x| = |y|
- x_i = y_i \quad \forall 1 \le i \le n
Operazioni sui linguaggi
- Unione
- Intersezione
- Complemento
- Differenza
- Concatenazione
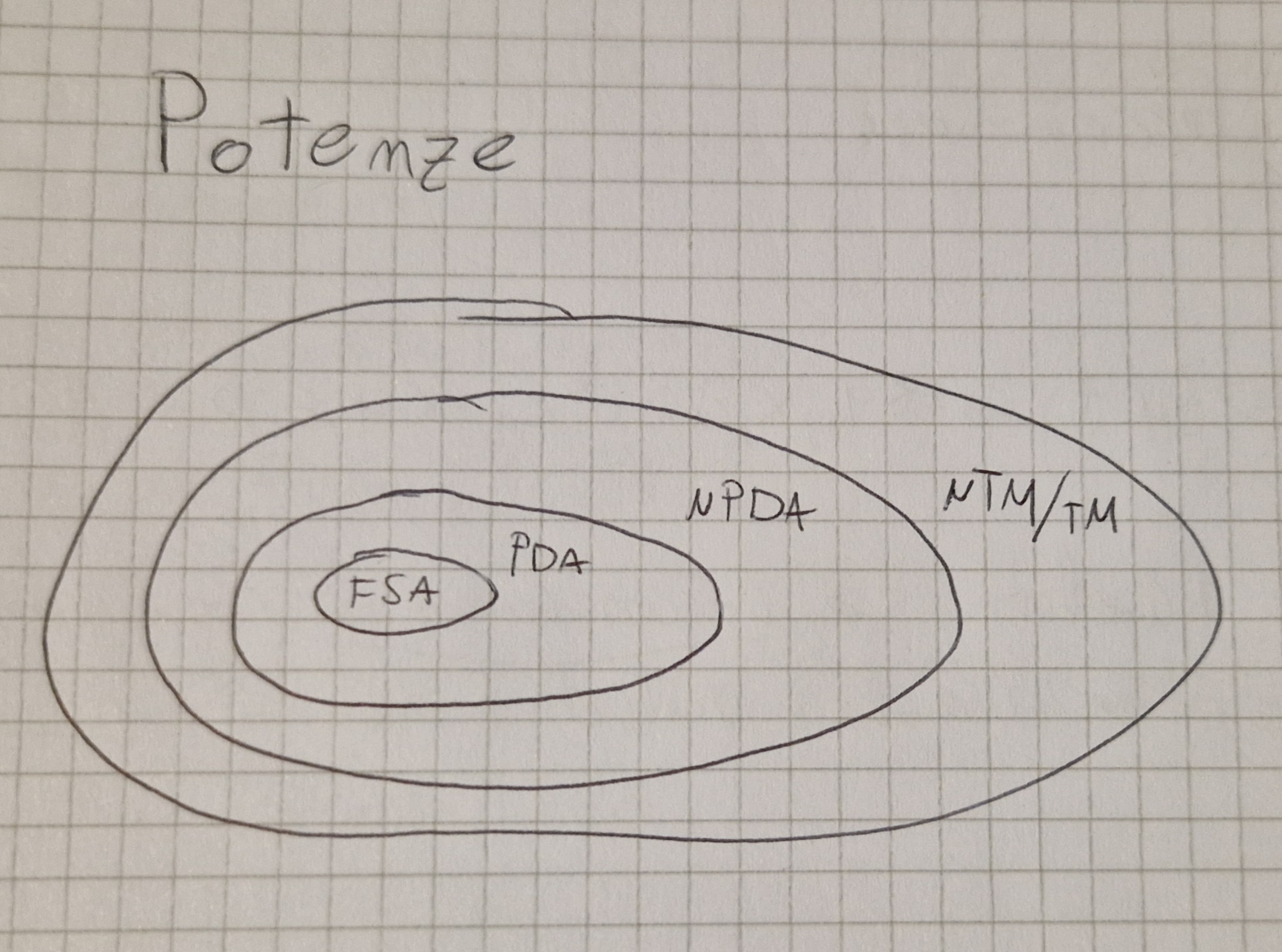
- Potenze n-esime
- Chiusura di Kleene
Prima di iniziare delle spiegazioni useremo le stringhe L_1 e L_2 così composte:
L_1 = \{ \varepsilon, a, b, c, bc, ca \} \\ L_2 = \{ ba, bb, bc, ca, cb, cc \}
Bene partiamo con la carrellata di operazioni.
Unione (L_1 \bigcup L_2)
L_1 \bigcup L_2 = \{ \varepsilon, a, b, c, ba, bb, bc, ca, cb, cc\} tutti gli elementi SENZA ripetizioni.
Intersezione (L_1 \bigcap L_2)
L_1 \bigcap L_2 = \{bc, ca\} SOLO elementi comuni.
Differenza (L_1 \setminus L_2 o L_1 - L_2)
L_1 \setminus L_2 = \{\varepsilon, a, b, c \} SOLO elementi NON comuni.
Complemento (L^c = A^* \setminus L)
A è l’alfabeto su cui L è definito.
* vuol dire tutte le ripetizioni possibili di quell’insieme, \varepsilon compreso.
L_1^c = tutte le stringhe su \{a, b, c\}* tranne stringhe di lunghezza 2 che iniziano con “b”, “c”.
Concatenazione (L_1 \cdot L_2 o L_1 L_2) NON è commutativa
L_1 \cdot L_2 = \{ba, bb, bc, ca, cb, cc, aba, abb, abc, aca, acb, acc, bba, bbb, bbc, bca, bcb, bcc, cba, cbb, cbc, cca, ccb, ccc, bcba, bcbb, bcbc, bcca, bccb, bccc, caba, cabb, cabc, caca, cacb, cacc\}
Potenza n-esima (L^n) concanetamento con se stesso n volte
L^i = \begin{cases} \varepsilon & i = 0 \\ L ^ {i - 1} \cdot L & i \gt 0 \end{cases}
La potenza È associativa.
Chiusura di Kleene
L^* = \bigcup_{n=0}^\infty L^n \\ \ \\ L^* = L^+ \bigcup L^0 = L^+ \bigcup \{\varepsilon\} \\ \ \\ L^+ = \bigcup_{n=1}^\infty L^n \\ \ \\ L^+ = L \cdot L^* \\ \ \\ \{\varepsilon\} \not = \emptyset \\
Automi a stati finiti
FSA (Finite State Automaton)
Un FSA ha un insieme finito di stati ovvero un numero limitato di configurazioni.
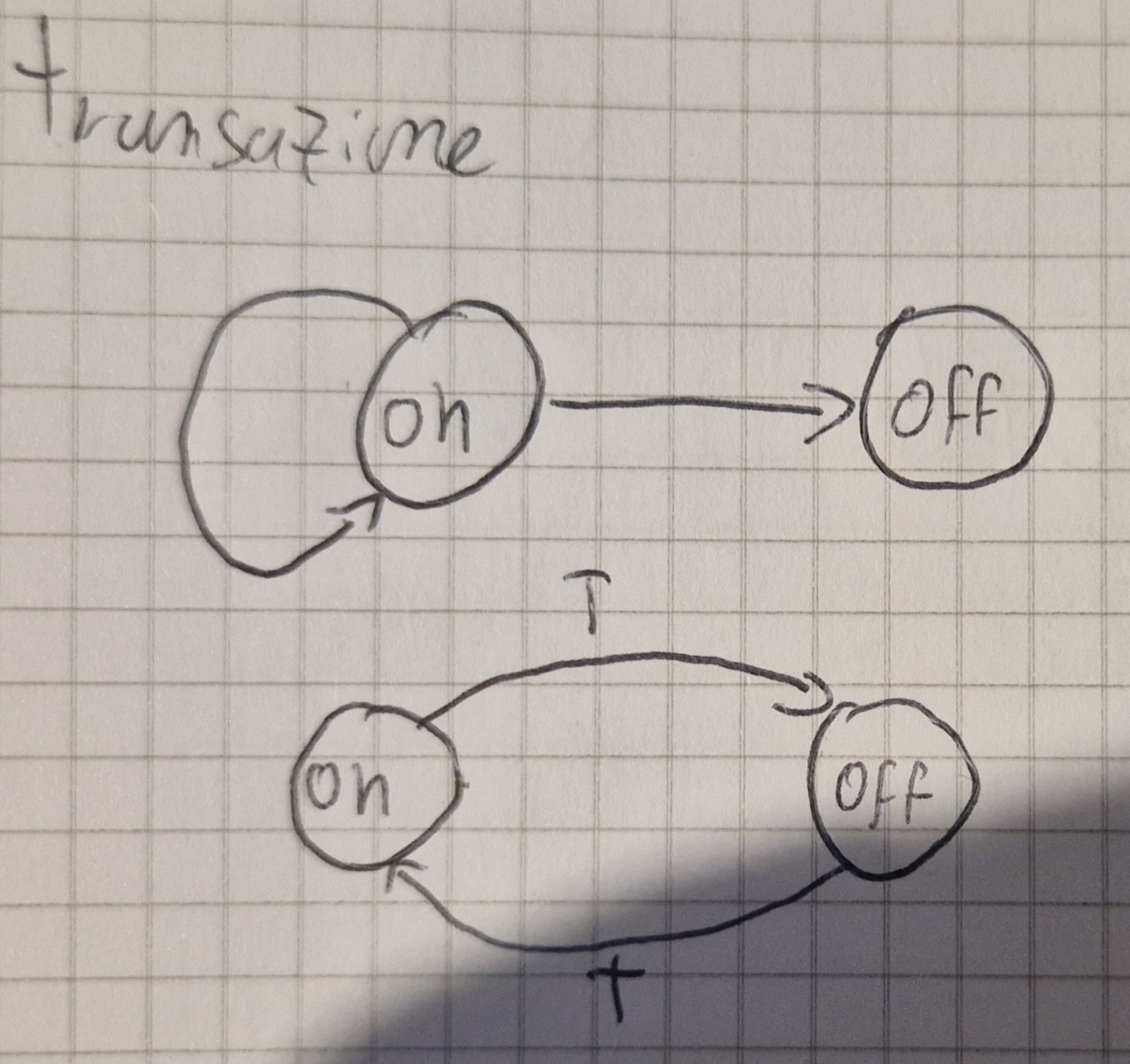
Es.
- {ON, OFF}
- {Canali TV}
Un FSA è definito su un alfabeto (a, b, c o anche on, off, anche 1, 2, 3, insomma simboli o parole che noi definiamo come “input” anche C o Java possono essere definiti come tale).
Quando si riceve un input, il sistema cambia il suo stato (transizione).
Gli FSA sono rappresentati tramite una tupla \lang Q, A, \delta, q_0, F \rang:
- Q insieme finito di stati
- A alfabeto di ingresso
- \delta funzione di transizione
- q_0 \in Q stato iniziale
- F \subseteq Q insieme stati finali
Per far sì che gli FSA riconoscano un linguaggio è necessario:
- Sapere le condizioni iniziali del sistema
- Sapere gli stati finali ammisibili
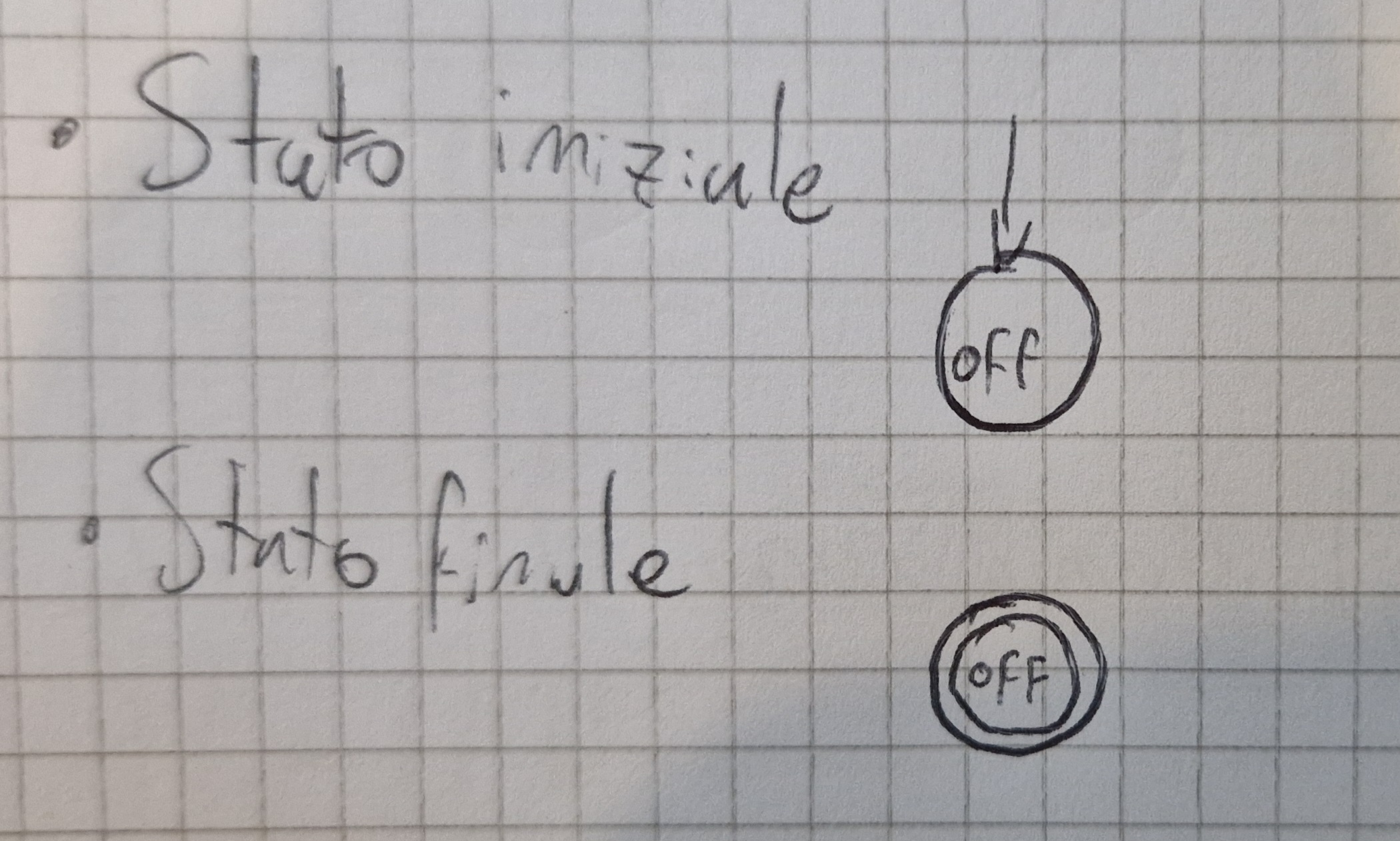
Una sequenza di mosse è di accettazione se raggiunge uno degli stati finali.
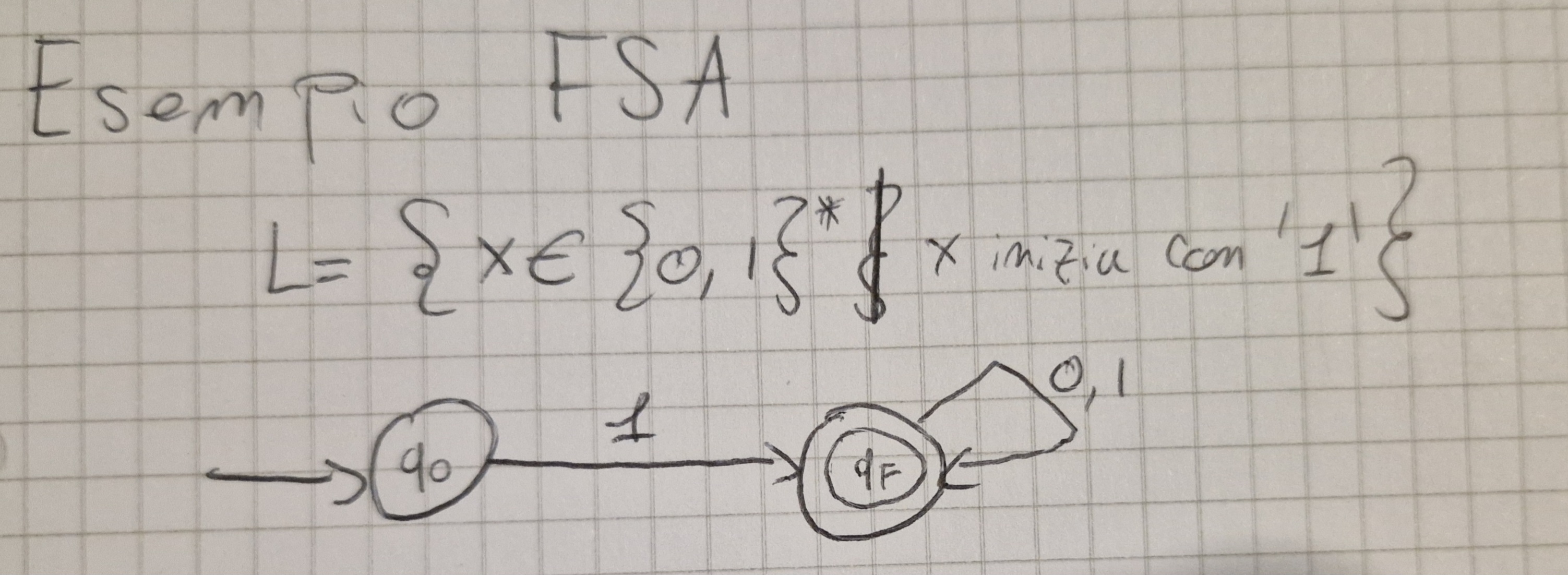
Esempio di un FSA:
Trasduttori a stati finiti
FST (Finite State Transducer)
Sono FSA con 2 nastri.
È una tupla \lang Q, I, \delta, q_0, F, O, \eta \rang:
- \lang Q, I, \delta, q_0, F \rang come gli accettori (FSA)
- O alfabeto di uscita
- \eta \colon Q \times I \longrightarrow O^*
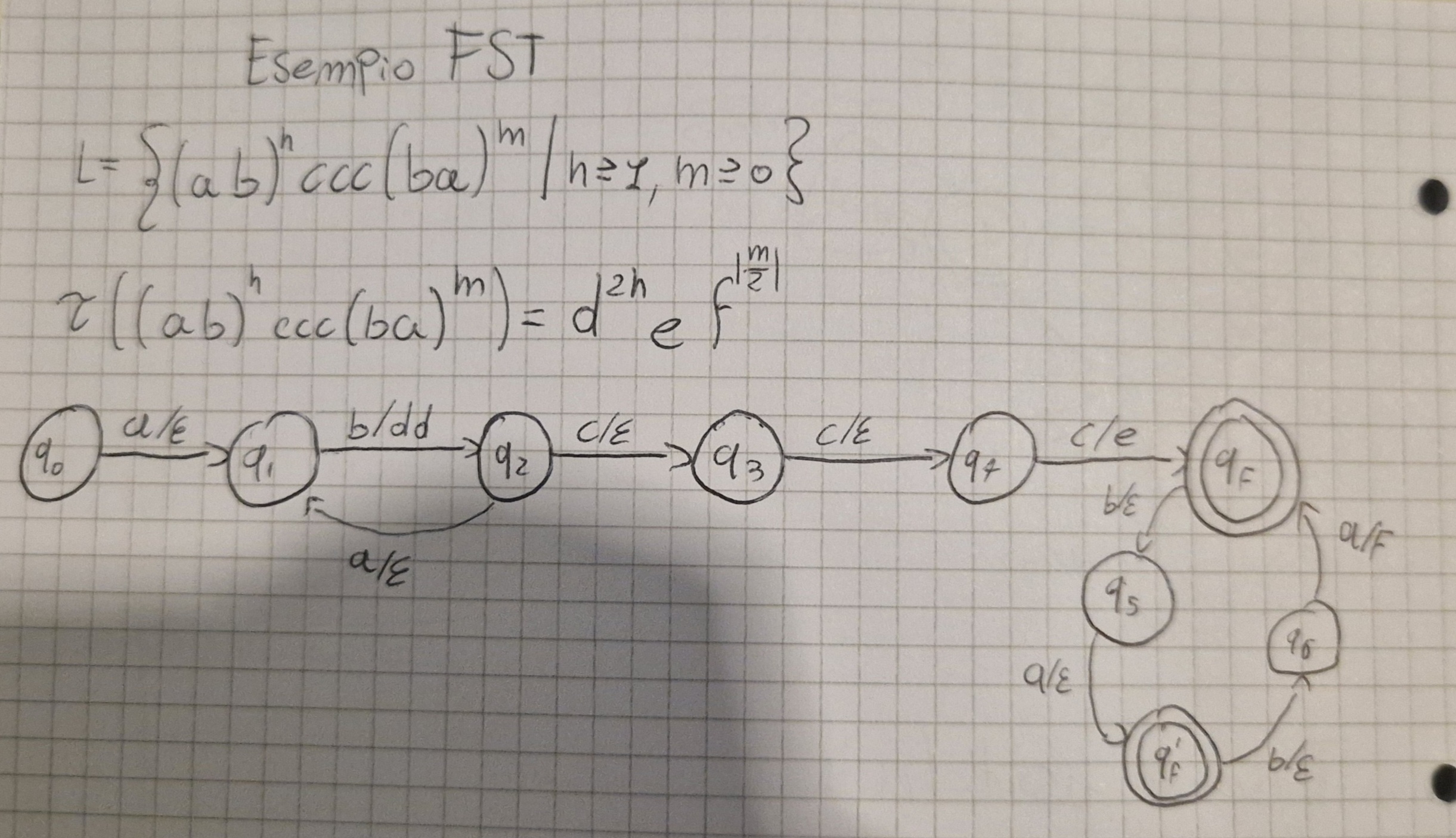
Esempio FST
Pumping Lemma
Se in un sistema a stati finiti si va da uno stato q_1 a q_1 (ovvero si attraversa un ciclo) vuol dire che lo si può fare n volte.
Perciò se:
x \in L e |x| \ge |Q| \implies q \in Q \land w \in I^+:
- x = ywz
- \delta^*(q, w) = q
Dunque:
- \forall n \ge 0 yw^nz \in L
Conseguenze:
L = \empty se \exist x \in L \iff \exist y \in L, |y| \lt |Q|
|L| = \infty se \exist x \in L |Q| \impliedby |x| \lt 2|Q|
Problemi:
- Per “contare” un numero n molto grande servirebbe memoria infinita
Operazioni su FSA
N.B. se un sistema è chiuso rispetto a un operazione vuol dire che il risultato è sempre parte dell’insieme.
Operazioni:
- Intersezione ( \bigcap )
- Unione ( \bigcup )
- Complemento ( ^c )
Sono operazioni CHIUSE negli FSA.
PDA (PushDown Automata)
Sono FSA con una pila.
La stringa d’ingresso x è accettata se:
- il PDA la legge tutta
- Quando finisce si trova in uno stato di accettazione
Un PDA è una tupla \lang Q, I, \Gamma, \delta, q_0, Z_0, F \rang:
- Q insieme finito di stati
- I alfabeto di ingresso
- \Gamma alfabeto di pila
- \delta funzione di transizione
- q_o \in Q è lo stato iniziale
- Z_0 \in \Gamma simbolo iniziale di pila
- F \subseteq Q insieme stati finiti
Esempio PDA:
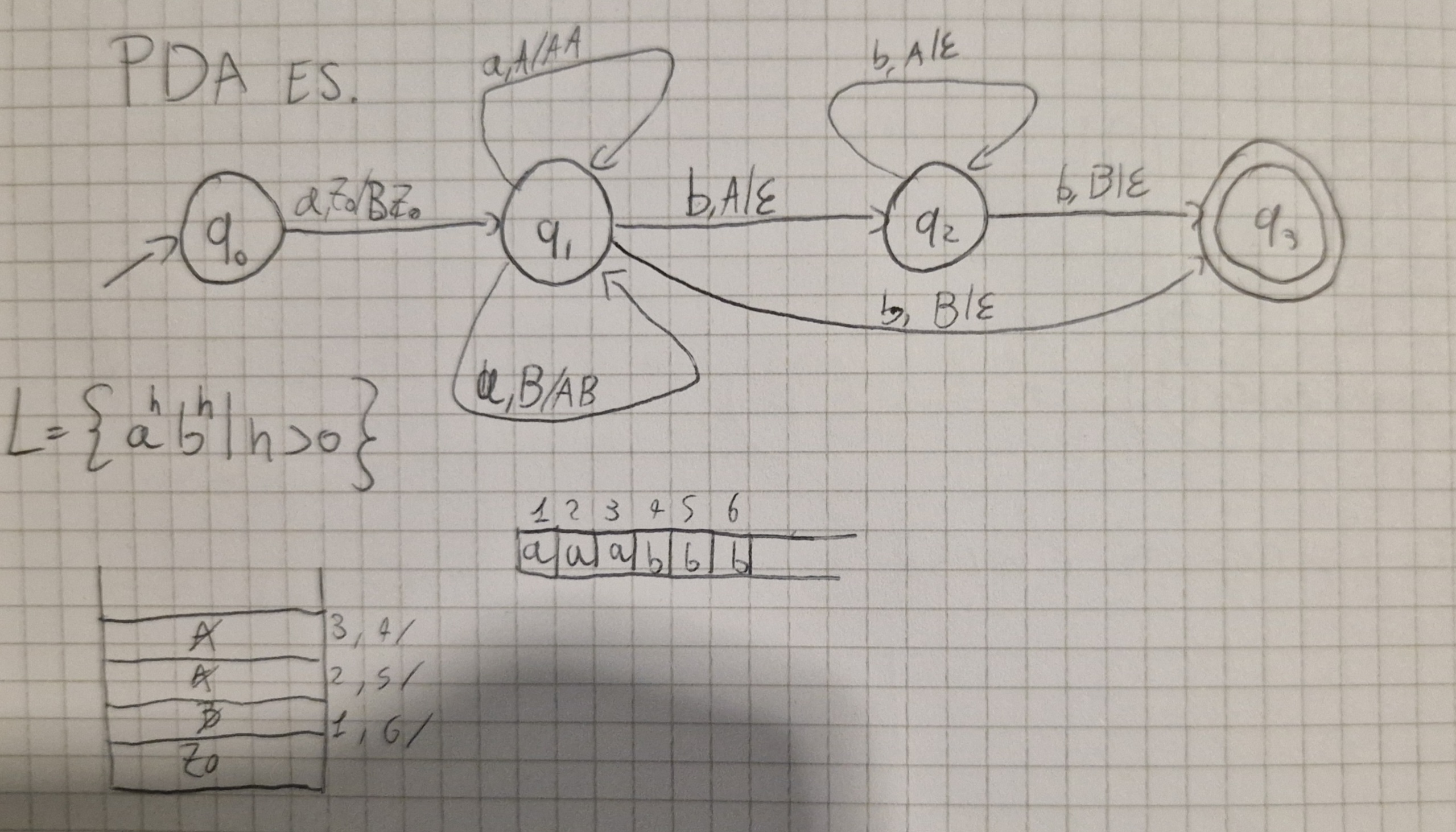
Configurazione
- Mostra lo stato corrente del dispositivo di controllo
- Posizione della stringa d’ingresso
- La pila
È una tripla \lang q, x, \gamma \rang
- q \in Q stato corrente dispositivo
- x \in I^* posizione non letta della stringa d’ingresso
- \gamma \in \Gamma^* stringa simboli di pila
Le transizioni tra configurazioni (\vdash) mostra come commutare tra un PDA e un altro
Esempio
Dato \delta(q, i, A) = \lang q', \alpha \rang è definita
c = \lang q, x, \gamma \rang \vdash c'= \lang q', x', \gamma \rang
- \gamma = A \beta
- x = iy
allora
- \gamma' = \alpha \beta
- x' = y
Condizione di accettazione
\forall x \in I^* (x \in L \iff \exist q \exist \gamma c_0 = \lang q_0, x, Z_0 \rang \vdash^* c_f = \lang q, \varepsilon, \gamma \rang \land q \in F)
La stringa viene accettata se c’è un cammino coerente che va sallo stato iniziale a uno stato finale.
PDA VS FSA
- Gli FSA NON riconoscono a^n b^n i PDA si
- Ogni linguaggio regolare (FSA) è riconosciuto da PDA
- I PDA sono più potendi dei FSA
I PDA non si fermano sempre dopo le mosse, ogni PDA si può trasformare in un PDA aciclico (si ferma sempre dopo le mosse).
PDT (PushDown Trasducer)
I PDT sono una tupla \lang Q, I, \Gamma, \delta, q_0, Z_0, F, O, \eta \rang:
- \lang Q, I, \Gamma, \delta, q_0, Z_0, F \rang come nei PDA
- O alfabeto d’uscita
- \eta \colon Q \times (I \bigcup \{ \varepsilon\} ) \times \Gamma \to O^*
Configurazione <q, x, \gamma, z>:
- \lang q, x, \gamma \rang come nei PDA
- z stringa già scritta sul nastro d’uscita
Condizione di accettazione:
\forall x \in I^* \forall z \in O^* (x \in L \land z = \tau(x) \iff \exist q \exist \gamma \colon c_0 = \lang q_0, x, Z_0, \varepsilon \rang \vdash^* c_f = \lang q, \varepsilon, \gamma, z \rang \land q \in F )
La traduzione è definita se e solo se x è accettata.
Esempio di PDT
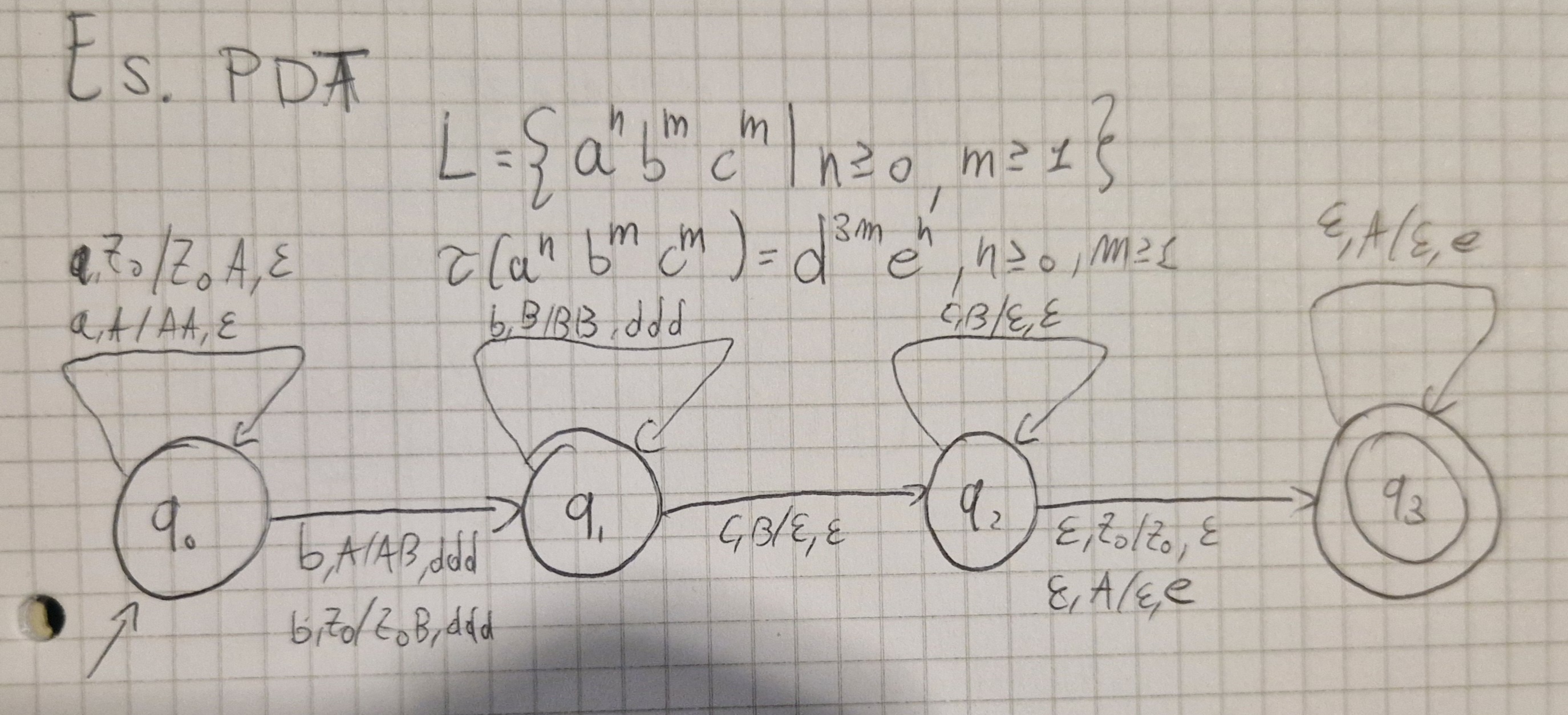
I PDT NON sono chiusi rispetto a Unione, Intersezione e Complemento.
Turing Machine (TM)
I PDA NON riconoscono a^n b^n c^n o a^n b^n \cup a^n b^{2n}.
La pila è una memoria distruttiva, letto un elemento viene eliminato.
C’è bisogno di NASTRI DI MEMORIA.
Le TM usano i nastri come memorie:
- Non distruttivi
- Scorrevoli in entrambi i sensi
I nastri sono sequenze infinite di celle con “Blank” (segnato come “\cancel{b}”, “_” o “-”).
Mosse
Uguali a prima con aggiunta di:
Spostamento testine dichiarato con 3 movimenti:
- Sposta a destra (R)
- Sposta a sinistra (L)
- Fermo (S)
Si esplicita SEMPRE.
Le TM sono una tupla \lang Q, I, \Gamma, \delta, q_0, Z_0, F \rang:
- Q insieme finito di stati
- I alfdabeto di ingresso
- \Gamma alfabeto di memoria
- \delta funzione di transizione
- q_0 \in Q stato iniziale
- Z_0 \in \Gamma simbolo iniziale di memoria
- F \subseteq Q insieme stati finali
Esempio di TM
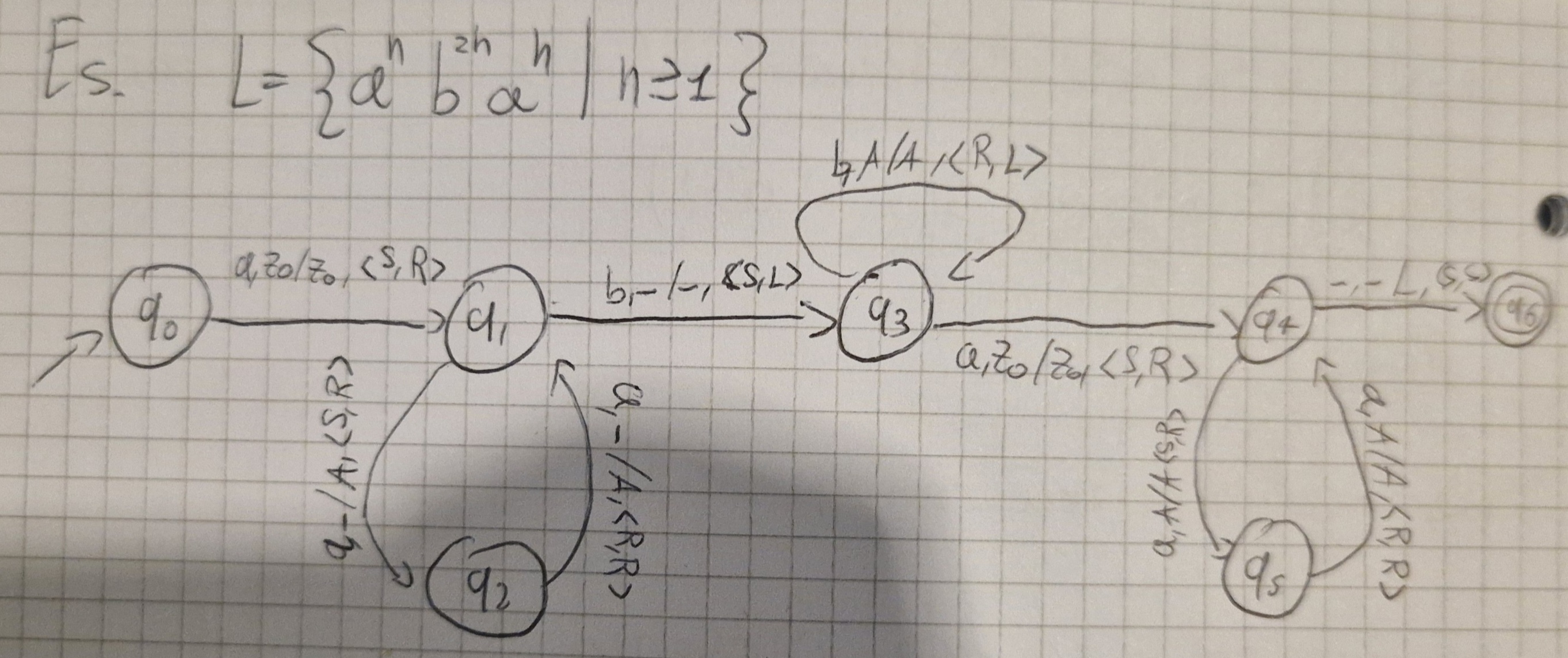
La Configurazione di una TM con k nastri è una (k+2)-tupla:
c = \lang q, x \uparrow iy, \alpha_1 \uparrow A_1 \beta_1, \dots, \alpha_k \uparrow A_k \beta_k \rang
- q \in Q
- x, y \in I^*, i \in I
- \alpha_r, \beta_r \in \Gamma^*, A_r \in \Gamma \forall r \quad 1 \le r \le k
- \uparrow \notin I \cup \Gamma
\uparrow indica la posizione della testina.
Condizione di accettazione:
\exist q \exist x' \exist i \exist y \exist \alpha_1 \exist A_1 \exist \beta_1 \dots \exist \alpha_k \exist A_k \exist \beta_k \colon c_0 = \lang q_0, \uparrow x, \uparrow Z_0, \dots, \uparrow Z_0 \rang \vdash_m^* c_F = \lang q, x'\uparrow iy, \alpha_1 \uparrow A_1 \beta_1, \dots, \alpha_k \uparrow A_k \beta_k \rang con q \in F e x = x'iy
TM VS PDA
- a^n b^n c^n NON sono riconosciuti da PDA ma da TM
- Se un linguaggio è riconosciuto da PDA allora è riconosciuto da TM
I linguaggi accettati da TM sono detti ricorsivamente enumerabili.
TM e Macchine di Von Neumann (VNM)
La differenza sta nell’accesso alla memoria:
- TM : Sequenziale
- VNM : Diretto
Il tipo di accesso NON cambia la potenza.
Le TM possono simulare le VNM.
Operazioni TM
Le TM sono chiuse rispetto a:
- Intersezione (\bigcap)
- Unione (\bigcup)
- Concatenazione
- Stella di Kleene
NON sono chiuse rispetto a:
- Complemento
- Differenza
Se esistessero TM acicliche sarebbero chiuse al complemento, il problema sta dove le computazioni non terminano.
TM Trasduttrice
Le TM trasuttrici a k nastri sono una tupla di 9 elementi \lang Q, I, \Gamma, O, \delta, \eta, q_0, Z_0, F \rang:
- \lang Q, I, \Gamma, \delta, q_0, Z_0, F \rang come le TM
- O alfabeto d’uscita
- \eta funzione d’uscita
N.B. Le testine di uscita si muovono in 2 direzioni:
- Destra (R)
- Ferme (S)
Esempio di TM traduttrice
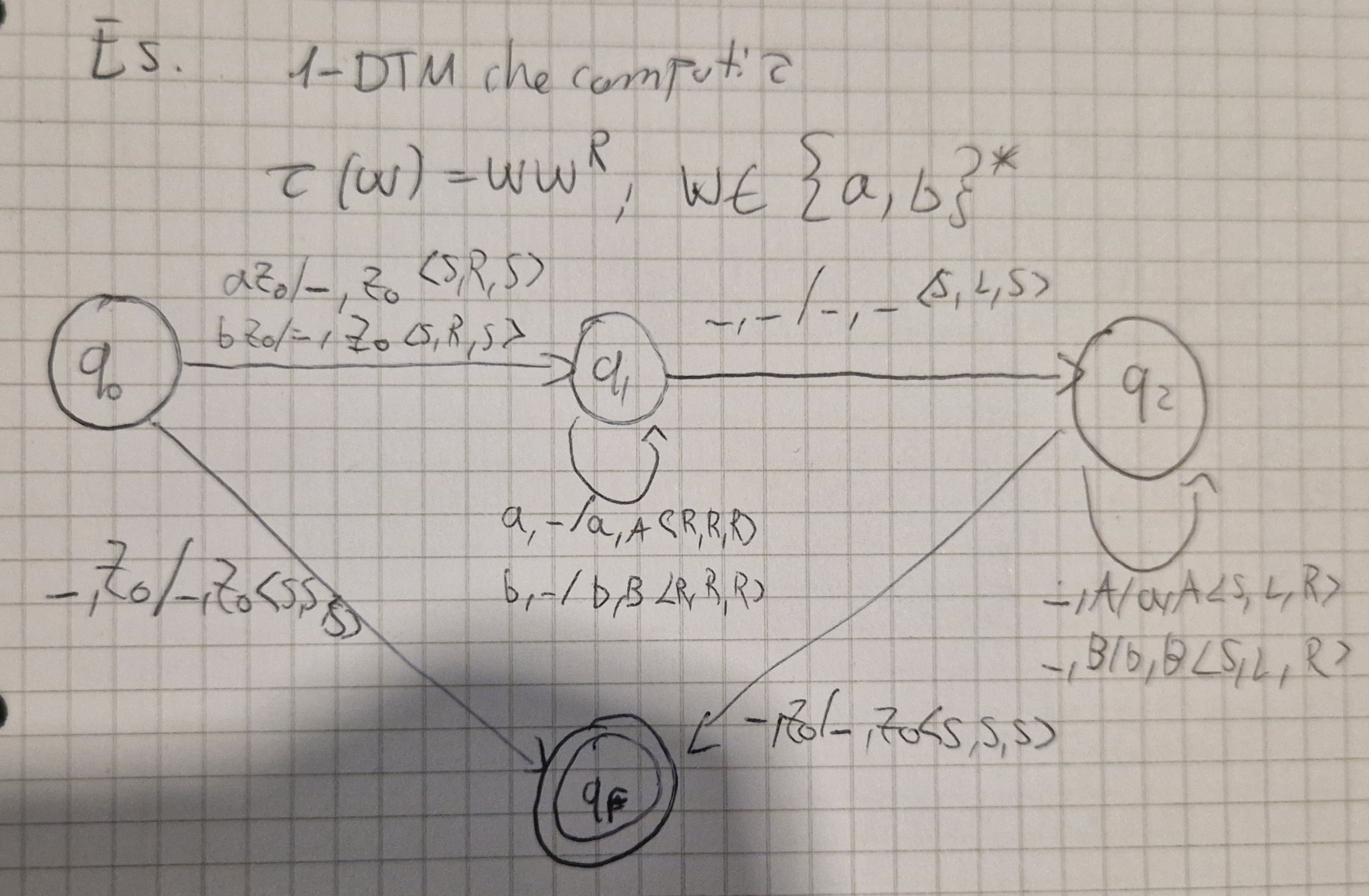
Configurazione
c = \lang q, x \uparrow iy, \alpha_1 \uparrow A_1 \beta_1, \dots, \alpha_k \uparrow A_k \beta_k, u \uparrow o \rang
- \uparrow \in I \bigcup \Gamma \bigcup o
Le TM possono:
- Riconoscere linguaggi
- Tradurre linguaggi accettati
- Calcolare funzioni
Le TM sono computer con accesso sequenziale alla memoria (Modello astratto).
Le TM possono avere nastri a n dimensioni.
N.B. Più dimensioni NON aggiungono potenza.
Modelli non deterministici
Di solito un algotimo ha una sequenza deterministica.
Il non deterministmo (ND) è un modello di computazione, utile per algoritmi di ricerca.
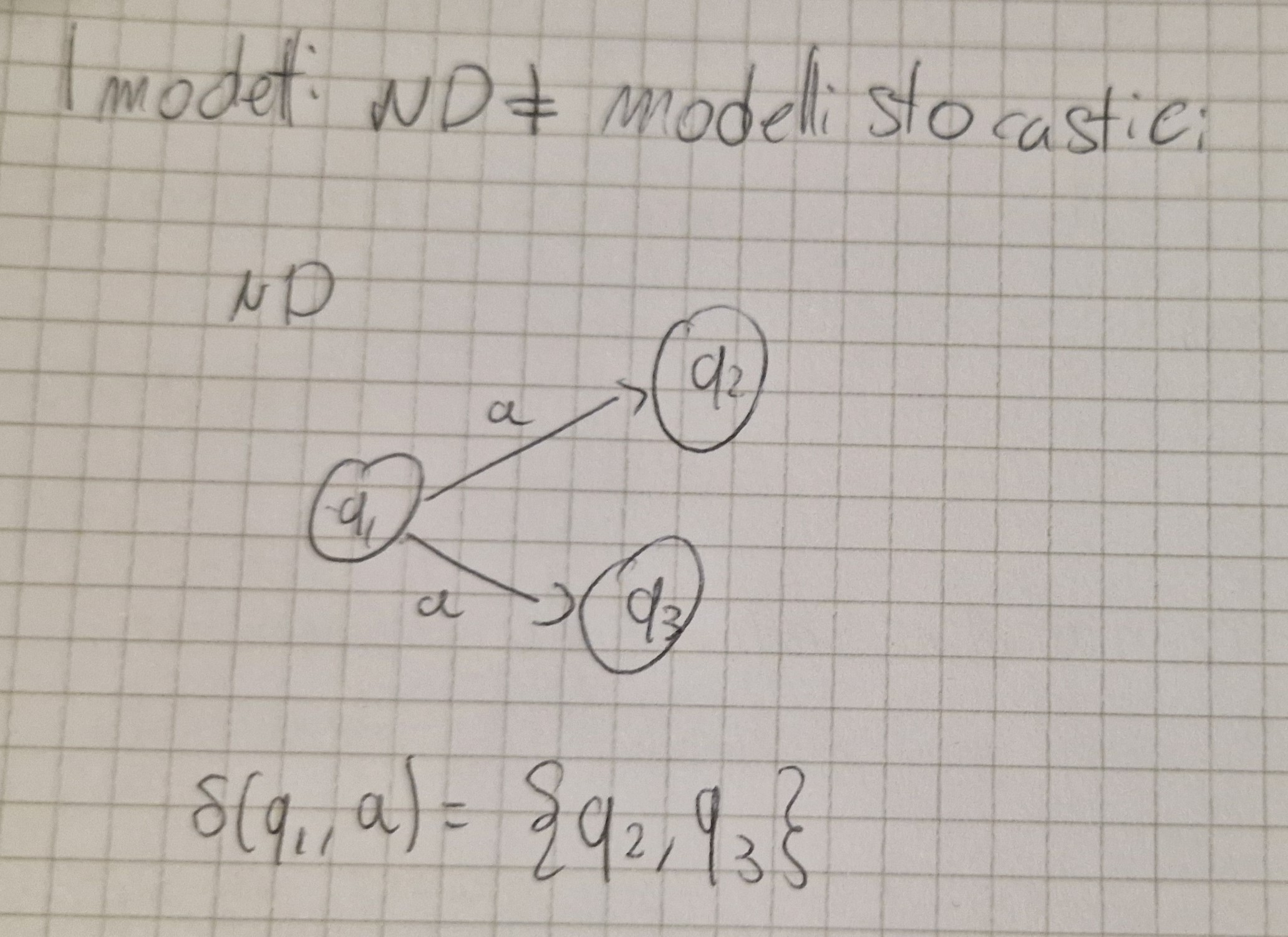
NFSA
Gli NFSA sono gli FSA non deterministici e sono una tupla : \lang Q, I, \delta, q_0, F \rang
- \lang Q, I, q_0, F \rang uguali a FSA
- \delta \colon Q \times I \to \mathcal{P} (Q)
\delta^* (q, \varepsilon) = \{q\} \\ \delta^* (q, y, i) = \bigcup \delta\{q', i\}
Condizione di accettazione
x \in L \iff \delta^* (q_0, x) \bigcap F \not ={\emptyset}
Basta che una vada a buon fine.
ND esistenziale
\delta^* (q_0, x) \subseteq F
DFA VS NFA
- Stesso potere
- Da un NFA si può sintetizzare automaticamente un DFA
Se A_{ND} = \lang Q, I, \delta, q_0, F \rang \implies A_{D} = \lang Q_D, I, \delta_D, q_{0D}, F_D \rang
- Q_D = \mathcal{P}(Q)
- \delta_D (q_D, i) = \bigcup \delta (q, i)
- q_{0D} = \{q_0\}
- F_D = \{q_D | q_D \in Q_D \land q_D \bigcap F\not ={\emptyset} \}
Perchè il ND ? (già è difficile di suo ora ci complichiamo la vita)
Gli NFA hanno pari potenza di DFA, ma non sono inutili (purtroppo):
- A volte gli NFA sono più semplici
- Possono essere esponenzialmente più piccoli (NFA a 5 stati nel peggiore dei casi è un DFA a 2^5 stati)
Esempio di NFA
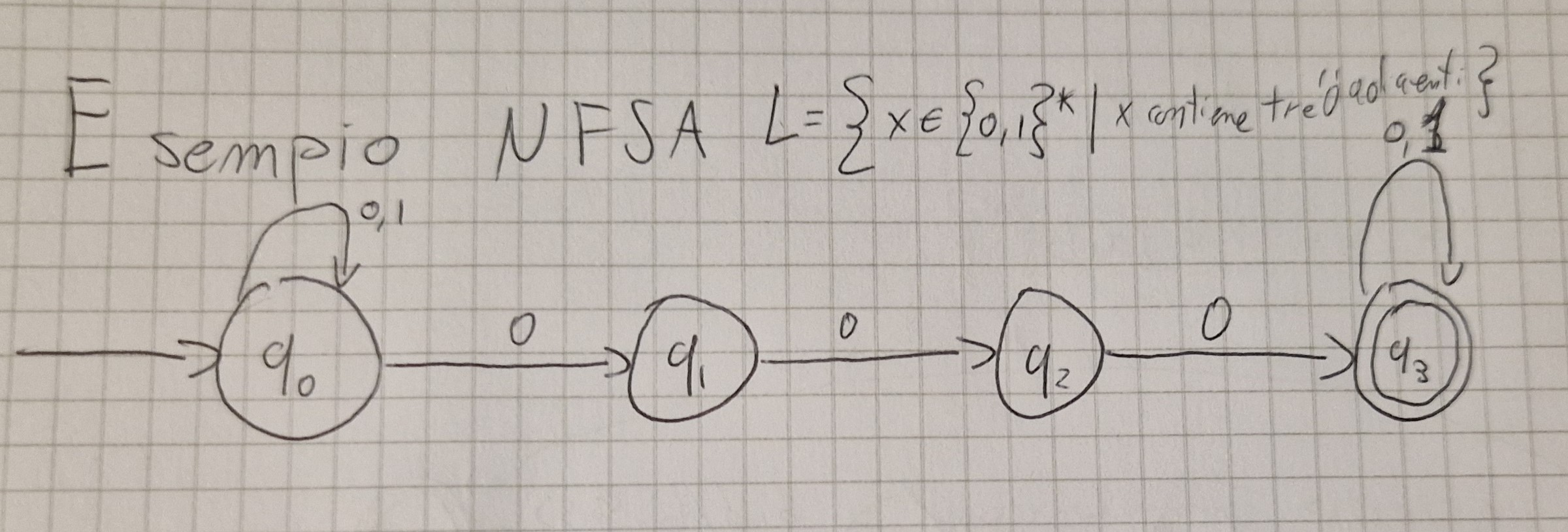
TM non deterministici (NTM)
Per definire una NTM occorre cambiare la funzione di transizione e la funzione di traduzione.
- Elementi uguali alla DTM
- \delta \colon (Q-F) \times I \times \Gamma^k \to \mathcal{P}(Q \times \Gamma^k \times \{R, L, S\}^{k+1})
- \eta \colon (Q-F) \times I \times \Gamma^k \to \mathcal{P}(O \times \{R, S\})
Esempio NTM
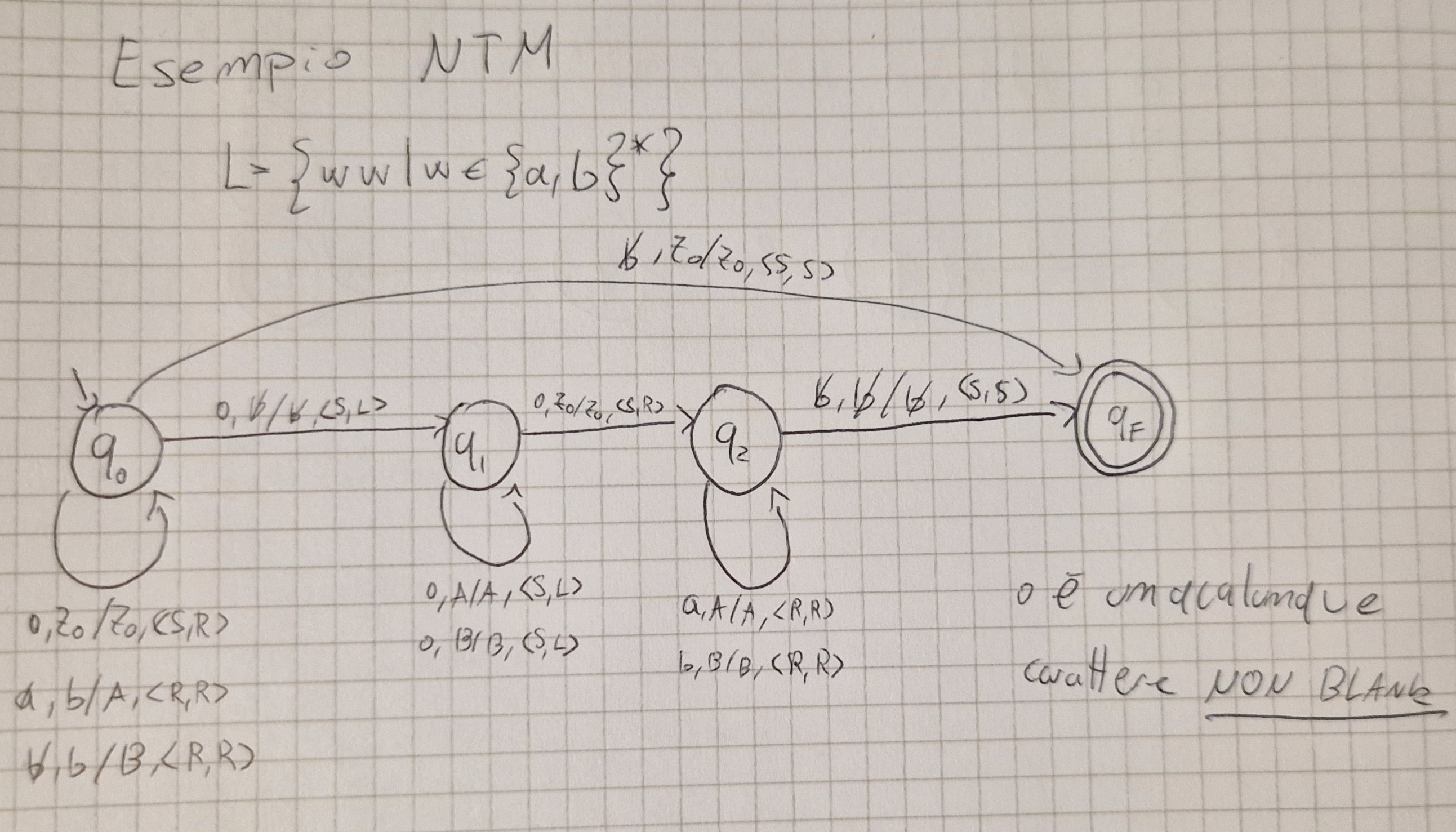
Condizione di accettazione
Una stringa è accettata se e solo se esiste unna computazione con uno stato di accettazione.
Che cosa è la visita dell’albero computazionale ?
Diverse modalità :
- In profondità (Depth-first)
- In ampiezza (Breadth-first)
Si può costruire una DTM che visita un albero livello dopolivello ma è un processo molto lungo e noioso.
ND NON aggiunge potere alle TM
PDA non deterministici (NPDA)
L e \varepsilon-mosse avevano il seguente vincolo:
\delta(q, \varepsilon, A) \not ={\bot}\implies\delta(q, i, A) = \bot; \forall i \in I
Senza di esso i PDA sarebbero intrinsicamente ND.
Un NPDA è una tupla \lang Q, I, \Gamma, \delta, q_0, Z_0, F \rang
- \lang Q, I, \Gamma, q_0, Z_0, F \rang come nel PDA
- \delta è la funzione di transazione definita come: \delta \colon Q \times (I \bigcup \{\varepsilon\}\times \Gamma \to \mathcal{P_F}(Q \times \Gamma^*))
\mathcal{P_F} indica i sottoinsiemi finiti di Q \times \Gamma^*
Esempio di NPDA
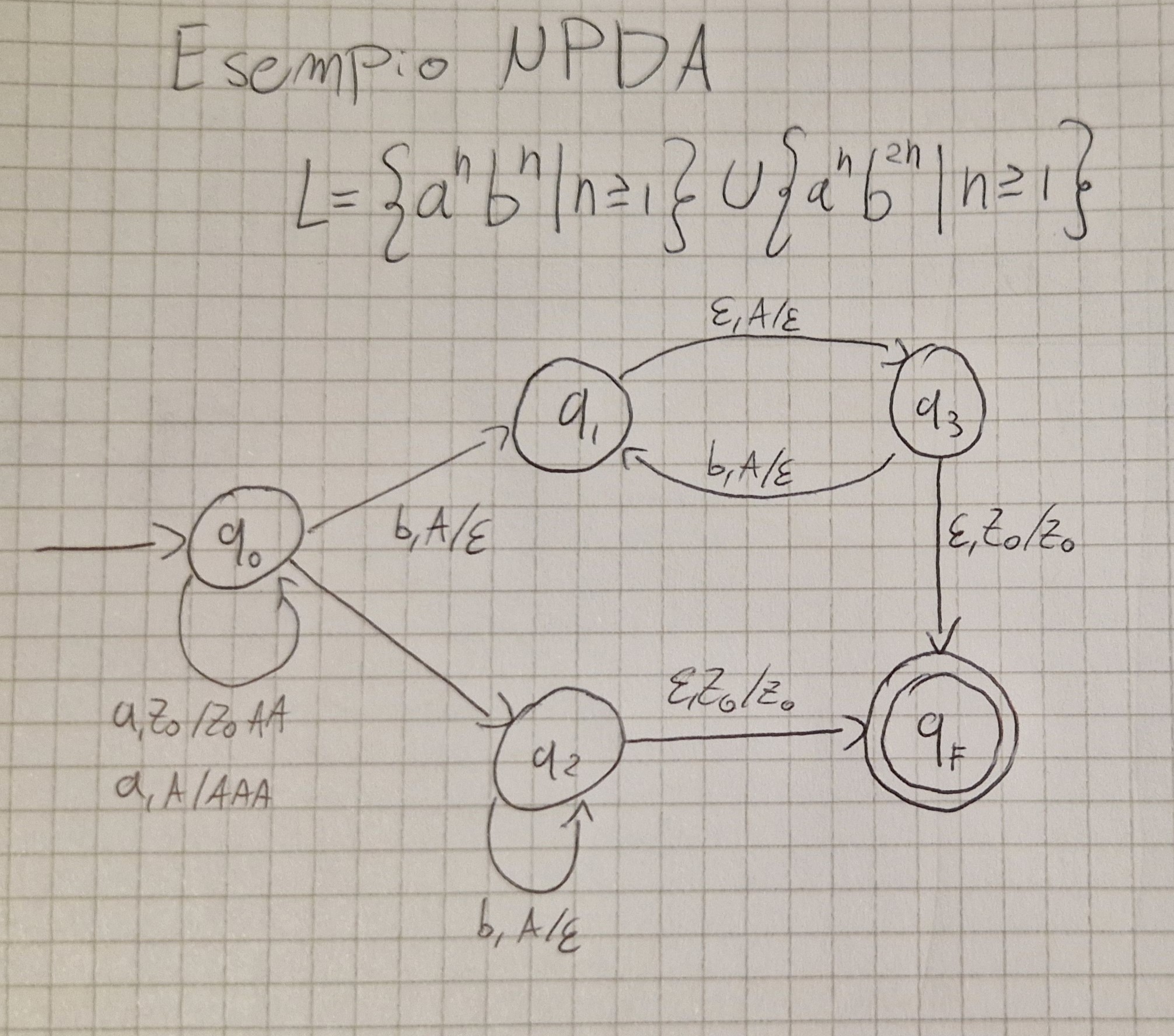
Condizione di accettazione
Dato un NPDA:
\forall x \in I^* (x \in L(P) \iff \exist q \exist \gamma c_0 = \lang q_0, x, Z_0 \rang \vdash^* c_F = \lang q, \varepsilon, \gamma \rang e q \in F)
Una stringa è accettata se c’è un cammino coerente con x che va dallo stato inizio a uno di fine.
ND noi PDA aggiunge potere, riconosce \{ a^nb^n | n\ge 1\} \bigcup \{a^nb^{2n} | n \ge 1\}
I linguaggi riconoscibili dai PDA sono detti context-free.
DPDA chiusi rispetto al complemento.
NON chiusi rispetto unione, intersezione e differenza.
NPDA chiusi rispetto unione.
NON chiusi rispetto intersezione, complemento e differenza.
| Proprietà chiusura | FSA | DPDA | NPDA | TM |
|---|---|---|---|---|
| Unione | SI | NO | SI | SI |
| Intersezione | SI | NO | NO | SI |
| Complemento | SI | SI | NO | NO |
| Concanetazione | SI | NO | SI | SI |
| Stella di Klenee | SI | NO | SI | SI |
Grammatiche
Esistono 2 tipi di modelli:
- Modelli operazionali (Automi): Riconoscono/accettano, traducono e calcolano linguaggi.
- Modelli generativi (Grammatiche): Descrivono come generare un linguaggio.
I modelli generativi producono stringhe (grammatica).
Una grammatica è un insieme di parole per costruire le frasi di un linguaggio \to tramite riscrittura (insieme di metodi).
Regole linguistiche
Le regole linguistiche descrivono un “oggetto principale” con una sequenza di componenti.
I componenti vengono dettagliati fino ad andare alla base (vuol dire che es. da staccionata si arriva a Assi, Martello, Chiodi).
Una grammatica è una tupla \lang V_N, V_T, P, S \rang
- V_N alfabeto NON TERMINALE
- V_T alfabeto TERMINALE
- V = V_N \bigcup V_T
- P = \subseteq V_N^+ \times V^* insieme finito di regole di riscrittura
- S \in V_N è un particolare elemento di V_N chiamato assioma
Una grammatica genera un linguaggio sull’alfabeto V_T
Produzioni
Elemento di V_N^+ \times V^* (\lang \alpha, \beta \rang | \alpha \in V_N^+, \beta \in V^*)
Si indica con \alpha \to \beta
- \alpha sequenza simboli NON terminali.
- \beta sequenza (potenzialmente vuota) di simboli (terminali o non)
Gerarchia Chomsky
Esistono 4 tipi di grammatiche
| Tipo | Nome | Produzioni | Macchine |
|---|---|---|---|
| 3 | Regolari | (Destre) A \to \alpha, A \to aB (A \to \varepsilon) con A,B \in V_N, a \in V_T | FSA |
| 2 | Context-free | A \to B, A \in V_N | NPDA |
| 1 | Context-sensitive e monotone | S \to \varepsilon, \alpha A \beta \to \alpha \gamma \beta con A \in V_N, \alpha, \beta, \gamma \in V^+ (ora monotone) \alpha \to \beta con \vert \alpha \vert = \vert \beta \vert | Automi lineari (NTM usano uno spazio di memoria proporzionale all’input) |
| 0 | Generali o non ristrette | P \subseteq V_N^+ \times V^+ | TM |
Reazioni di derivazione immediata
\alpha \implies \beta (\beta è ottenuta immediatamente da \alpha)
- \alpha \in V_N^+ e \beta \in V^*
se e solo se
\alpha = \alpha_1 \alpha_2 \alpha_3, \beta = \alpha_1 \beta_2 \alpha_3 e \alpha_2 \to \beta_2 \in P
\alpha_2 riscritta come \beta_2 nel contesto \lang \alpha_1, \alpha_3 \rang
Es. (Context-Sensitive)
V_N = \{S,A, B, C, D\}\\ V_T = \{a, b, c\}\\ S\\ P = \{S \to AB, BA \to cCD, CBS \to ab, A \to \varepsilon\}\\ aaBAS \implies aacCDS \\ bcCBSAdd \implies bcabAdd
Linguaggio generato
Data G = \lang V_N, V_T, P, S \rang
\forall x (x \in L(G) \iff x \in V_T^* \land S \implies(+) x)
Il linguaggio generato da G è l’insieme di tutte le stringhe:
- Solo simboli terminali
- Derivante da S in n numeri di passi con n \ge 1
ES. (Context-Free)
G_2 = \lang \{S\}, \{a, b\}, \{S \to a Sb | ab\}, S \rang \\ S \to aSb |ab = S \to aSb, S \to ab
Derivazioni
S \implies ab
$S aSb aabb $
S \implies aSb \implies aaSbb \implies aaabbb
Generalizzo L(G_2) = \{a^nb^n|n> 0\}
Regular Grammar (RG) VS FSA
Sia A un FSA, si può costruire un RG G ad esso equivalente.
G genera esattamente lo stesso linguaggio riconosciuto da A.
Le RG, FSA e espressioni regolari descrivono lo stesso linguaggio in modelli diversi.
Le context-free grammar (CFG) sono identiche alle Backus-Naus Form (BNF) usate per definire la sintassi dei linguaggi di programmazione.
Le grammatiche regolari sono anche non contestuali
I linguaggi possono essere rappresentati tramite molti modelli tra cui :
- Pattern
- Espressioni Regolari (RE)
Pattern
È una tripla \lang A, V, p \rang
- A è un alfabeto
- V insieme di variabili | A \bigcap V = \emptyset
- p è una stringa su A \bigcup V detta pattern
Il pattern genera un linguaggio che ha tutte le stringhe di A ottenute da p sostituendo ogmi variabile in p con una stringa su A.
Es. \lang \{0, 1\}, \{v_1, v_2\}, v_1v_1 \circ v_2 \rang
- Stringhe che iniziano con 0 (v_1 = \varepsilon)
- Stringhe che iniziano con una stringa su A ripetuta due volte, seguita da uno 0 e da una qualunque stringa (inclusa \varepsilon)
RE: sintassi e semantica
Definizione di un RE su un alfabeto A \colon
- \emptyset è una RE
- \varepsilon è una RE
- ogni simbolo di A è una RE
Siano r e s due RE, allora:
- (r.s) è una RE
- r^* è una RE
- Nient’altro è una RE
Es.
((0.(0|1)^*)|((0|1)^*.0)) è una RE su \{0, 1\}
- stringhe che iniziano con 0
- stringhe che finiscono con 0
RE e Pattern
Le RE hanno la stessa idea dei Pattern ma diverso potere.
RE \not ={Pattern}.
\{xx | x \in \{0, 1\}^*\} NO RE
Pattern corrispondente \lang \{0, 1\}, \{x\}, xx \rang
Linguaggio denotato da 0^*1^* NON ESPREMIBILE tramite Pattern.
RG e RE
RG = RE.
RE POSIX (Linux/Unix)
Caratteri meta: ( ) . [ ] ^ $ * + | { }
N.B. “.” indica qualunque carattere, NON concatenazione.
[\alpha] indica un singolo carattere \in \alpha ([abc] indica \{a, b, c\}).
[\^\ \alpha] negazione: qualunque carattere non in \alpha.
^ e $ indicano \varepsilon corrispettivamente all’inizio e alla fine della riga.
*, +, |, (, ) uguali a sempre.
“escape” ( $ indica il simbolo $).
\alpha ? indica \alpha opzionale.
\alpha \{n\} indica \alpha^n
\alpha \{n, m\} indica \alpha^n \bigcup \alpha ^{n+1} \bigcup \dots \bigcup \alpha^m
Logica
Esistono vari linguaggi logici :
- Logica Proposizionale
- FOL (First-Order Logic)
La logica è un formalismo “universale” e si applica in molti ambiti :
- Architetture (porte logiche)
- Ingegneria del software
- Linguaggi di programmazione
- Database
- AI
Gli insiemi possono essere visti come abbreviazioni di formule FOL.
Es.
\{a^nb^n | n \ge 0\} \to abbreviata di \forall x (x \in L \longleftrightarrow \exist n (n \ge 0 \land x = a^n.b^n))
x^n ?
\forall n \forall x ((n=0 \to x^n = \varepsilon) \land (n > 0 \to x^n = x^{n-1}.x))
Ora faremo un bell’ elenco di operazioni logiche, buon viaggio ; )
L_1 = a^*b^*
L_1 è il linguaggio delle stringhe su \{a, b\} con tutte le “a” all’inizio.
Più precisamente L_1 è:
- stringa vuota.
- composta da un prefisso “a” e un suffiso y (sempre in L_1).
- prefisso y (sempre in L_1) e un suffisso “b”.
Esprimibile come:
\forall x (x \in L_1 \longleftrightarrow (x = \varepsilon) \lor \exist y (x=ay \land y \in L_1) \lor \exist y (x=yb \land y \in L_1))
L_2 = a^*b^*c^*
Una stringa appartiene a L_2 se è:
- in L_1
- in L_3 (b^*c^*)
- composta da un prefisso 'a' e da un suffisso y
- composta da un prefisso y e da un suffisso 'c'
In FOL:
\forall x (x \in L_2 \longleftrightarrow (x \in L_1) \lor (x \in L_3) \lor \exist y (x = ay \land (y \in L_2 \lor y \in L_3)) \lor (x=yc \land (y \in L_2) \lor y \in L_1))
Esempio
L_4 = \{x \in \{a,b\}^* |numero\ di\ 'a'\ uguale\ al\ numero\ di \ 'b'\}
- \#(x,a) arietà 2, conta il numero di occorenze del simbolo 'a' nella stringa x
In FOL: \forall x (x \in L_4 \longleftrightarrow \# (x,a)= \# (x,b))
MFO: Logica monadica del prim’ordine
- I linguaggi esprimibili mediante MFO sono chiusi rispetto a unione, intersezione e complemento
- In MFO non si può esprimere il linguaggio L_p fatto di tutte le sole parole di lunghezza pari con l = \{a\}
- MFO è strettamente meno potente degli FSA
- MFO chiuso rispetto alla *
- La formula MFO a(0) \land a(1) \land last(1) definisce L_{aa} fatto della sola parola \{aa\} di lunghezza 2.
- Abbiamo che L_p = L_{aa}^*
- MFO definisce linguaggi star-free, definibili tramite unione, intersezione, complemento e concatenazione di linguaggi finiti.
MSO: Logica monadica del secondo ordine
Può avere lo stesso potere degli FSA basta permettere di quantificare sui predicati monadici
Ammettiamo formule del tipo \exist x(\phi), x è una variabile il cui dominio è l’insieme dei predicati monadici
Assegnamento delle variabili del II ordine (insieme v_2) è una funzione v_2 : V_2 \to ([0..|w|-1])
- w, v_1, v_2 \vDash X(x) \ sse\ v_1(x) \in v_2 (x)
- w, v_1, v_2 \vDash \exist X (\phi) \ sse \ w, v_1, v_2' \vDash \phi \ per \ qualche \ v_2' \ con \ v_2'(Y); Y\not ={x}
La formula descrive il linguaggio L_p
\exist P (\forall x (\neg P(0) \land (\neg P(x) \Longleftrightarrow P(x+1))\land a(x)\land (last(x) \implies P(x))))
Per ogni FSA esiste un MSO equivalente
Da una MSO \phi è possibile costruire un FSA (Teorema di Büchi-Elgot-Trakhtenbrot)
I linguaggi definibili da formule MSO sono linguaggi regolari

Quando si programma una funzione è importante definire COSA FA.
Precondizione: indica cosa deve valere prima che la funzione sia invocata.
Postcondizione: indica cosa deve valere dopo che la funzione ha finito la propria esecuzione.
Struttura generale (notazione di Hoare)
- {Precondizione: Pre}
- {Programma: P}
- {Postcondizione: Post}
P deve essere tale che se Pre vale prima dell’esecuzione, allora Post vale dopo l’esecuzione.
Pre e Post possono essere definiti in diversi modi
- Linguaggio naturale
- Linguaggi per le asserzioni
- Linguaggi ad-hoc
\to FOL può essere usata per questo scopo.
Abbreviazioni logiche
y=x+1 \ \ \ x<y \land \neg \exist z (x<z \land z<y) N.B. è vero se x è l’ultima posizione
y=x+2 \ \ \ \exist z(z=x+1 \land y=z+1)
\forall k \in \mathbb{N}, k \ge 1 (k fissato NON si può quantificare !!!)
y=x+k : \ \ \exist z (z=x+(k-1) \land y= z+1)
First(x,P) = P(x) \land \forall y (y<x \implies \neg P(y))
Last (x,P) = P(x) \land \forall y (x<y \implies \neg P(y))
Next (x,y,P) = P(x) \land P(y) \land \forall z ((x<z \land z<y)\implies P(z))
Odd(Q,P) = \forall x (Q(x) \iff (First (x,y) \land \exist y \exist z (Next (z,x,P) \land Next (y,z,P) \land Q(y))))
OddCard(P)= \exists Q(Odd(Q,P) \land \forall x (Last(x,P) \implies Q(x)) \land \exist x P(x)) dice se |P| è dispari.
Vero sse Q \subseteq P \ Q contiene la I, II, V posizione di P.
Tabella dei Formalismi e Tipi di Chomsky
| Formalismo | Tipo Chomsky | Classe linguaggi | Potenza | Descrizione sintetica | ||||
|---|---|---|---|---|---|---|---|---|
| Espressioni regolari (RE) | Tipo 3 | Regolari | 🔹 Minima | Linguaggi descrivibili con unioni, concatenazioni, e star (es:
(a+b)*abb). |
||||
| Automatoni a stati finiti deterministici (DFA) | Tipo 3 | Regolari | 🔹 Minima | Modello equivalente alle RE; riconosce solo ling. regolari. | ||||
| Automatoni a stati finiti non deterministici (NFA) | Tipo 3 | Regolari | 🔹 Minima | Come DFA ma con nondeterminismo. Stessa potenza. | ||||
| Formule logiche monadiche (MFO) | Tipo 3 | Regolari | 🔹 Minima | Linguaggi esprimibili con logica del primo ordine monadica. | ||||
| Grammatiche libere da contesto (CFG) | Tipo 2 | Context-Free (CFL) | 🔸 Intermedia | Possono descrivere linguaggi annidati (es:
a^n b^n). |
||||
| Pushdown Automata (PDA) | Tipo 2 | Context-Free | 🔸 Intermedia | Modello con stack, equivalente alle CFG. | ||||
| Grammatiche dipendenti dal contesto (CSG) | Tipo 1 | Context-Sensitive (CSL) | 🔶 Alta | Ogni produzione non accorcia la stringa (\alpha \leq \beta). | ||||
| Lineari sensibili al contesto (LBA) | Tipo 1 | Context-Sensitive | 🔶 Alta | Turing Machine a memoria limitata alla lunghezza dell’input. | ||||
| Grammatiche generali / non restrittive | Tipo 0 | Ricorsivamente enumerabili | 🔺 Massima | Nessuna restrizione sulle produzioni. | ||||
| Macchine di Turing (TM) | Tipo 0 | Ricorsivamente enumerabili | 🔺 Massima | Qualsiasi linguaggio computabile. | ||||
| TM deterministica (DTM) | Tipo 0 | Ricorsivi (decidibili) | 🔺 Massima | TM che termina sempre. | ||||
| TM non deterministica (NTM) | Tipo 0 | Ric. enumerabili (semi-dec.) | 🔺 Massima | Può non terminare su input fuori dal linguaggio. |
Computabilità
Algoritmo di ricerca
Pre: l’array è ordinato.
Post: la variabile logica “found(un flag)” dev’essere vera sse l’elemento cercato esiste nell’array.
Pre \{\forall i (1 \le i \le n-1 \to a[i] \le a[i+1])\} \\ P \\ Post \{found \longleftrightarrow \exist i (1 \le i \le n \land a[i] = x)\}
Ordinamento
Pre: l’array NON contiene ripetizioni.
Post: l’array ottenuto è ordinato.
Formalmente
\{\neg \exist i, j (1 \le i \le n \land 1 \le j \le n \land i \not ={j} \land a[i] = a[j])\} \\ ORD \\ \{\forall i (1 \le i \le n-1 \to a[i] \le a[i+1])\}
Tesi di Church (Parte 1)
Non c’è nessun formalismoper modellare il calcolo meccanico che sia più potente della TM (o formalismi equivalenti)
Algoritmo: Procedura per risolvere problemi mediante un dispositivo di calcolo automatico.
Tesi di Church (Parte 2)
Ogni algoritmo può essere codificato mediante una TM (o formalismo equivalente)
Una TM può essere vista come un computer astratto, non programmabile, predisposto per un uso speciale.
Un insieme S può essere enumerato algoritmicamente (E) se possiamo trovare una biiezione tra S e \natnums.
- E: S \longleftrightarrow \natnums
Esempio
\{a,b\}^*
\varepsilon\ a\ b\ aa\ ab\ ...
0\ 1\ 2\ 3\ 4\ ...
Le TM possono essere enumerate algoritmicamente
Ipotesi:
- TM a nastro singolo
- Alfabeto fissato A (esempio\ |A|=3, A=\{0, 1,\_ \})
Esempio: TM con due stati

2^2=4 stati finali possibili.
Quante funzioni f: D \to R ? \to |R|^{|D|}
Con |Q| = 2, |A|=3, (2 * 3+3+1)^{(2*3)} = 19^6 con 2 stati considerando i 2^2 scelte di stati finali, abbiamo (al più) 19^6 * 2^2 TM.
Ordiniamo TM: \{M_0,...,M_{19^6*2^2 -1} \}
Otteniamo un’enumerazione E: \{TM\} \to \natnums
E(M) è detto numero di Gödel di M e E è una Gödelizzazione
Le TM modellano computer programmabili? Si
- Consideriamo la Macchina di Turing Universale (UTM)
UTM computa g(y, x)=f_y(x)
funzione calcolata dalla y-esima TM sull’ingresso x.
Possiamo codificare g(y,x) come una g^{(n)} = g(d^{-1}(n)) con n= d(y,x), (y,x) = d^{-1} (n)
Le TM computano tutte le funzioni da \natnums a \natnums?
No, ci sono funzioni che possono essere computate dalla UTM.
Esistono 2^{\alef_0} funzioni f: \natnums \to \natnums.
\alef_0 si legge “alef con zero”
Il “problema dell’arresto” (halting problem)
- Costruisco un programma
- Gli do dei dati in ingresso
- So che in generale il programma potrebbe non terminare la propria esecuzione
In termini di TM:
g(y,x) =1\ se\ f_y(x) \not ={\bot}, g(y,x)=0\ se \ f_y(x)=\bot
C’è TM che calcola g?
No
Dimostrazione per diagonalizzazione
Listiamo le funzioni calcolabili da \natnums a \natnums e i loro valori, disponendo ogni valore f_y(x) in una tabella:

Definiamo una funzione \phi: \natnums \to \natnums che differisce dalla diagonale in ogni valore.
Nessuna TM può decidere se, data una generica TM M e un generico ingresso x, M si arresta con l’ingresso x.
Lemma importante
h'(x)= se f_x(x)\not ={\bot} allora 1 altrimenti 0
Un problema non risolvibile può avere un caso particolare risolvibile.
Se un problema è risolvibile, una generalizzazione può non essere risolvibile.
Problemi di decisione
Domanda con due possibili risposte: si e no.
Semidecidibile se c’è un algoritmo che dice si se la risposta è si
- può andsre in loop se la risposta è no
Insiemi Ricorsivi
Concentriamoci sui problemi a risposta binaria:
Problema= x appartiene all’insieme S? (S \le N)
C_S(x)=\ se \ x \in S\ allora\ 1\ altrimenti\ 0
Un insieme S è ricorsivo sse la sua funzione caratteristica è computabile.
S è ricorsivamente enumerabile sse:
- S è l’insieme vuoto, o
- S è l’immagine di una funzione g_s totale e computabile
S=l_{g_s}=\{x|x=g_s(y),y\in \natnums\} \\ \implies \\ S=\{g_s(0), g_s(1), g_s(2),...\}
Teorema (1/2+1/2=1)
- Se S è ricorsivo, allora è RE
- S è ricorsivo sse sia S sia il suo complemento S^\wedge = N-S sono RE
La classe di insiemi decidibili è chiusa rispetto al complemento.
Teorema del punto fisso di Klenne
Sia t una funzione totale e computabile. Allora si può sempre trovare un intero p tale che f_p=f_{t_{(p)}}
- La funzione f_p è detta punto fisso di t
Teorema di Rice
Sia f un insieme di funzioni computabili l’insieme &S& degli indici delle TM che calcolano le funzioni di F
S=\{x|f_x \in F\}
è decidibile sse:
- o F = \emptyset
- o F è l’insieme di tutte le funzioni computabili
\to in tutti i casi non banali S non è decidibile!
Dal teorema di RIce
Implicazioni negative
- C’è una lista sconfinata di problemi interessanti la cui indecidibilità segue banalmente dal teorema di Rice.
Dato F=\{g\}, per Rice non è decidibile se una generica TM calcoli g o meno.
Teorema di Rice (variante)
Sia S \subseteq \mathbb{N} tale che
- S \not = \empty
- S \not = \mathbb{N}
- se s \in S e la TM n-esima è equivalente alla TM m-esima allora m \in S (S è l’insieme di tutte e sole le codifiche di certe TM/prog/funz. computabili)
Allora S non è decidibile.
Esempio di utilizzo
Esistano TM M e M’ tali che M è equivalente a M’
H = \{ n \in \mathbb{N} | M=\lang n \rang \ e\ M(\varepsilon) \downarrow \} è decidibile ?
- H \not = \empty: ci sono TM che terminano su \varepsilon
- H \not = \mathbb{N}: ci sono TM che NON terminano su \varepsilon
- se M=M' e \lang M \rang = n e \lang M' \rang = n e n \in H allora H (\varepsilon) \downarrow e poichè M=M' anche M'(\varepsilon) \downarrow e dunque n' \in H
Quindi Rice è soddisfatto e H NON è decidibile.
Riduzione di problemi
Un problema P' è ridotto a un problema P se un algoritmo per risolvere P viene usato per risolvere P'
- P è risolvibile
- C’è un algoritmo che, per ogni data istanza di P'
- Determina una corrispondente istanza di P
- Costruisce algoritmicamente la soluzione dell’istanza di P' dalla soluzione dell’sistanza di P
Riduzione (Variante)
Siano A,B \subseteq \mathbb{N} e f: \mathbb{N} \to \mathbb{N}, f è una riduzione da A a B.
- f è TOTALE e COMPUTABILE
- se n \in A allora f(a) \in B
- se n \not \in A allora f(a) \not \in B
Teorema
Se A non è ricorsivo allora B non è ricorsivo.
Caratteristiche di alcuni linguaggi
Regolari \implies Ricorsivi
Context-free \implies Ricorsivo
Context-Sensitive \implies Ricorsivo
Ricorsivo \implies Ricorsivamente enumerabile
Ciò implica che sicuramente un linguaggio ricorsivo è R.E. ma non vuol dire che lo sia sempre anche il contrario
Complessità del calcolo
Per la tesi di Curch-Turing, un problema è calcolabile o meno indipendentemente dallo strumento usato.
Per la complessità del calcolo ?
- Una somma unaria ha efficienza diversa da una di basa b > 1
- Calcolare una traduzione y=T(x) decidendo se \exist z \in L_\tau = \{x \ y | y=\tau (x)\} può essere molto meno efficiente del calcolare la traduzione in qualche caso.
Data la computazione c_0 \vdash c_1 \vdash c_2 \vdash ... \vdash c_r di M (a k nastri) deterministica.
La complessità temporale è T_M (x)=r se M termina in c_r
- \infty se non termina.
M è deterministica \implies computazione unica sull’ingresso x
Complessità spaziale
S_M(x) = \Sigma _{j=1}^k max_{i \in \{0,...,r\}} (|a_{ij}|)
Somma della quantità massime occupate
\forall x: \dfrac{S_M (x)}{k} \le T_M (x)
Notazione
\Omicron-grande : limite asintotico superiore
\Omega-grande: limite asintotico inferiore
\Theta-grande: limite asintotico sia superiore che inferiore
\Omicron-grande
Data g(n), \Omicron(g(n)) è l’insieme \Omicron(g(n))=\{f(n) | \exist c > 0, n_0 >0\ tali\ che\ \forall n>n_0, 0 \le f(n) \le c*g(n)\}
\Omega-grande
Data g(n), \Omega(g(n)) è l’insieme \Omega(g(n))=\{f(n) | \exist c > 0, n_0 >0\ tali\ che\ \forall n>n_0, 0 \le c*g(n) \le f(n) \}
\Theta-grande
Data g(n), \Theta(g(n)) è l’insieme \Theta(g(n))=\{f(n) | \exist c_1 > 0, c_2 >0, n_0 >0\ tali\ che\ \forall n>n_0, 0 \le c_1*g(n) \le f(n) \le c_2*g(n) \}
Proprità notevoli
f(n) \in \Theta(g(n)) \iff f(n) \in \Omicron(g(n)) \land f(n) \in \Omega (g(n))
Transitività
f(n) \in \Theta(g(n)) \land g(n) \in \Theta(h(n)) \implies f(n) \in \Theta (h(n))
f(n) \in \Omicron(g(n)) \land g(n) \in \Omicron(h(n)) \implies f(n) \in \Omicron(h(n))
f(n) \in \Omega(g(n)) \land g(n) \in \Omega(h(n)) \implies f(n) \in \Omega(h(n))
Riflessività
f(n) \in \Theta(f(n))
f(n) \in \Omicron(f(n))
f(n) \in \Omega(f(n))
Simmetria: f(n) \in \Theta(g(n)) \iff g(n) \in \Theta(f(n))
Simmetria trasposta: f(n) \in \Omicron(g(n)) \iff g(n) \in \Omega(f(n))
\Theta è una relazione di equivalenza.
Teorema
Se L è accettato da una TM M a k nastri in S_M (n), \forall c \in \reals^+ posso costruire una TM M' a k nastri che accetta L con S_{M'} < c*S_M(n)
Teorema
Se L è accettato da una TM M a k nastri in S_M(n), posso costruire una TM M' a 1 nastro (non nastro singolo) che accetta L con S_{M'}(n) = S_M(n)
Teorema
Se L è accettato da una TM M a k nastri in S_M(n), \forall c \in \reals^+ posso costruire una TM M' a 1 nastro accetta L con S_{M'}(n)< c*S_M(n)
Teorema
Se L è accettato da una TM M a k nastri in T_M(n), \forall c \in \reals^+ posso costruire una TM M' a k+1 nastri accetta L con T_{M'}(n) = max (n+1, c*T_M(n))
Macchina RAM
La macchina RAM è dotata di un nastro di lettura In e uno di scrittura Out come la TM.
È dotata di una memoria con accesso a indirizzamento diretto N[n], n \in \natnums al posto dei nastri di memoria: l’accesso non necessita di scorrimento delle celle.
Le istruzioni di un programma usano normalmente come sorgente il primo operando e come destinazione N[0]
Riconoscere L=\{wcw^R\}
T_{RAM}(n) = \Theta (n)
S_{RAM}(n) = \Theta (n)
Ricerca Binaria T_{RAM}(n)=\Theta(log(n))
Ricerca di 2^{2n}
Input: una sequenza ordinata di interi ed un numero da cercare in essa.
Output: 1 se l’elemento cercato esiste nella sequenza, 0 altrimenti.
Consideriamo il caso del calcolo di 2^{2n} con una RAM
read (n);
x=2;
for (int i=0; i<n; i++)\ x=x*x;
write(x);
Complessità temporale: T_{RAM} (n)= k_1+k_2+nk_3+k_4= \Theta (n)
Servono 2^n bit per scrivere il risultato !!!
Complessità a costo logaritmico: T_{RAM} (n)= \Omicron(log(n)+n(2^{n-1}+2^{2n-2}+2^n+3log(n))+2^n)=\Omicron(n2^{2n-2})
(Tesi) di correlazione polinomiale
Sotto “ragionevoli” ipotesi di criterio di costo, se un problema è risolvibile mediante il modello M_1 con complessità c_1(n), allora è risolvibile da un qualsiasi altro modello (turing equivalente) M_2 con complessità c_2(n) \le \pi (c_1(n)), dove \pi(*) è un opportuno polinomio.
Algoritmi
Si usa pseudocodice
Esempio: Ordinamento
INSERTION-SORT(A) \\ for\ j :=2\ to \ A.length \\ key:=A[j] \\ //inserisce\ A[j]\ nella\ sequenza\ ordinata\ A[1...j-1] \\ i:=j-1 \\ while\ i>0\ and\ A[i]>key \\ A[i+1]:=A[i] \\ i:=i-1 \\ A[i+1]:=key
Visto che questa lezione si basa su scrivere codici e analizzarne solo certe parti io mi limiterò a scrivere le parti più importanti.
- Dati composti sono organizzati in oggetti
- Gli oggetti hanno degli attributi (il valore dell’attributo (attr.) di un oggetto x, scriviamo x.attr)
- Una variabile che corrisponde ad un oggetto è un puntatore all’oggetto.
I paramentri sono passati per valore.
Quando un oggetto viene passato come paramentro, ciò che viene passato è il puntatore all’oggetto.
La macchina RAM esegue gli algoritmi in pseudocodice.
Si adotta il criterio di costo costante (tempo costante c_i) ci concentriamo solo sulla complessità temporale.
Algoritmo ordinamento complessità temporale
T(n)=c_1n+c_2(n-1)+c_4(n-1)+c_5\Sigma_{j=2}^n t_j+c_7\Sigma_{j=2}^n(t_j-1)+c_8(n-1)
Se l’array è già ordinato T(n)=an+b \implies T(n) = \Theta (n)
Se ordinato ma in ordine decrescente T(n)=an^2+bn+c \implies T(n)=\Theta(n^2)
Merg-Sort (del tipo “divide et impera”)
Si ordina dividendo l’array in 2 sotto-array, si ordinano e si fondono.
Complessità di un algoritmo divide et impera
Equazione di ricorrenza
\begin{cases} \Theta (1)\ se\ n<c \\ D(n) + aT(n/b)+ C(n) \end{cases}
a si divide in sottoinsiemi di dimensione 1/b ognuno.
D(n) costo di dividere il problema, C(n) costo di ricombinare i sottoproblemi e T(n) è il costo per risolvere il problema totale.
Ricorrenza per Merge-Sort
T(n)= \begin{cases} \Theta (1)\ se\ n<2 \\ 2T(n/2)+\Theta(n)\ altrimenti \end{cases} \\ a=b=c=2, D(n)= \Theta(1), C(n)=\Theta(n)
Teorema dell’esperto (master theorem) \implies NON COPRE TUTTI I CASI
(a \ge 1, b \ge 1 \ e \ n/b\ è\ o\ \lfloor n/b \rfloor\ o\ \lceil n/b \rceil)
- Se f(n) = \Omicron (n^{log_ba-\varepsilon}) \varepsilon >0,\ allora\ T(n) = \Theta(n^{log_ba})
- Se f(n) = \Theta (n^{log_ba}),\ allora\ T(n) = \Theta(n^{log_ba}log(n))
- Se f(n) = \Omega (n^{log_ba+\varepsilon}) \varepsilon >0,\ e\ af(n/b) \le cf(n) per qualche c<1 e per tutti gli n grandi a sufficienza, allora T(n) = \Theta (f(n))
- af(n/b) \le cf(n) è detta regolarità
Teorema dell’esperto MERGE-SORT
T(n) = 2 T(n/2) + \Theta (n)
a=b=2 \\ f(n)=n \\ n^{log_ba}=n'=n
Secondo caso
T_{MERGE-SORT}(n)= \Theta (nlog(n))
Caso particolare
Se f(n) è una funzione \Theta (n^k) per qualche k:
- se k < log_ba, allora T(n)= \Theta (n^{log_ba})
- se k=log_ba, allora T(n)=\Theta (n^k log (n))
- se k>log_ba, allora T(n)=\Theta (n^k)
nel 3° caso la regolarità è verificata automaticamente.
Condizione di regolarità
Sia T(n) = T(n/2)+n(2-cos(n)), a=1\ b=2
f(n)=n(2-cos(n))=\Omega (n)>n^{log_ba}=\Theta (1)
HEAPSORT
È un algoritmo di ordinamento efficace (ordina in tempo \Theta (n log(n))) ma ordina sul posto.
Un heap binario è un albero quasi completo
Un max heap è un heap tale che \forall nodo x dell’albero, il valore contenuto nel padre di x è \ge del contenuto di x.
Complessità di MAX-HEAPIFY
T_{MAX-HEAPIFY} = \Omicron (n), n altezza albero = \Omicron(log(n)) poichè l’albero è quasi completo \implies T_{MAX-HEAPIFY}=\Omicron(log(n))
QUICKSORT (tipo “divide et impera”)
- Ordina sul posto.
- Caso pessimo complessità \Theta(n^2)
- In media \Theta (n log(n))
Albero di decisione (binario)

Ogni albero binario di altezza n ha un numero di foglie al più 2^n
TEOREMA
Ogni albero di decisione di ordinamento di n elementi ha altezza \Omega (nlog(n))
Ricorrenze di ordine costante
a_i intero \ge 0
T(n)= \begin{cases} \Theta (1)\ se\ n \le m \le h \\ \Sigma_{1\le i\le n} a_i T(n-i)+cn^k\ se\ n>m \end{cases} \\ a=\Sigma_{1\le i\le n} a_i
se a=1, allora T(n)= \Omicron(n^{k+1})
se a \ge 2, allora T(n) = \Omicron(a^n n^k)
Esempio T(n)=T(n-1)+\Theta(n) ottengo T(n) = \Omicron(n^2)
Versione ricorsiva di INSERTION-SORT
Conting-Sort
T= \Theta (n) \ S=\Theta (n)
Ordinamento per conteggio, NON per confronto.
Ipotesi: numeri naturali da 0 a k.

Strutture Dati
Le strutture dati sono usate per contenere oggetti.
Rappresentano collezioni di oggetti.
Spesso, ma non sempre, gli oggetti di una struttura dati hanno:
- Una chiave, per indirizzare l’oggetto
- Dati satelliti associati
Due tipi di operazioni sulle strutture dati:
- Operazioni che modificano la collezione
- Operazioni che interrogano la collezione
ELENCO OPERAZIONI
- SEARCH(S,k)
- INSERT(S,x)
- DELETE(S,x)
- MINIMUM(S)
- MAXIMUM(S)
- SUCCESSOR (S,x)
- PREDECESSOR(S,x)
Pila (Stack)
Collezione di oggetti sulla quale fare le seguenti operazioni:
- Controllare se è vuota
- Inserire elementi (PUSH)
- Togliere elementi (POP)
Si gestisce con la politica LIFO (Last In First Out).
Si può implementare come un array.
Coda (Queue)
Simile alla pila a FIFO (First In First Out)
Stesse operazioni:
- Controllare se è vuota
- Inserire elementi (ENQUEUE)
- Togliere elementi (DEQUEUE)
N.B. DEQUEUE restituisce l’elemento tolto
Anche la coda può essere implementata tramite array.
Liste (doppiamente) concatenate
È simile a una lista dinamica in cui ogni oggetto ha 3 attributi:
- key, contenuto dell’oggetto
- next, puntatore oggetto seguente
- prev, puntatore oggetto precedente
- x.next = NIL, x non ha successore
- x.prev = NIL, x non ha predecessore
Altri tipi di lista:
- Concatenate in modo singolo
- NO puntatore prev
- Ordinate
- l’ordinamento avviene tramite chiavi, dalla minore alla maggiore
- NON Ordinate
- Circolari
- .prev della testa punta alla coda, e .next della coda punta alla testa.
Dizionario: insieme dinamico che supporta solo le operazioni di INSERT,\ DELETE,\ SEARCH.
Si accede agli oggetti tramite le chiavi.
Si assume che le chiavi siano numeri naturali.
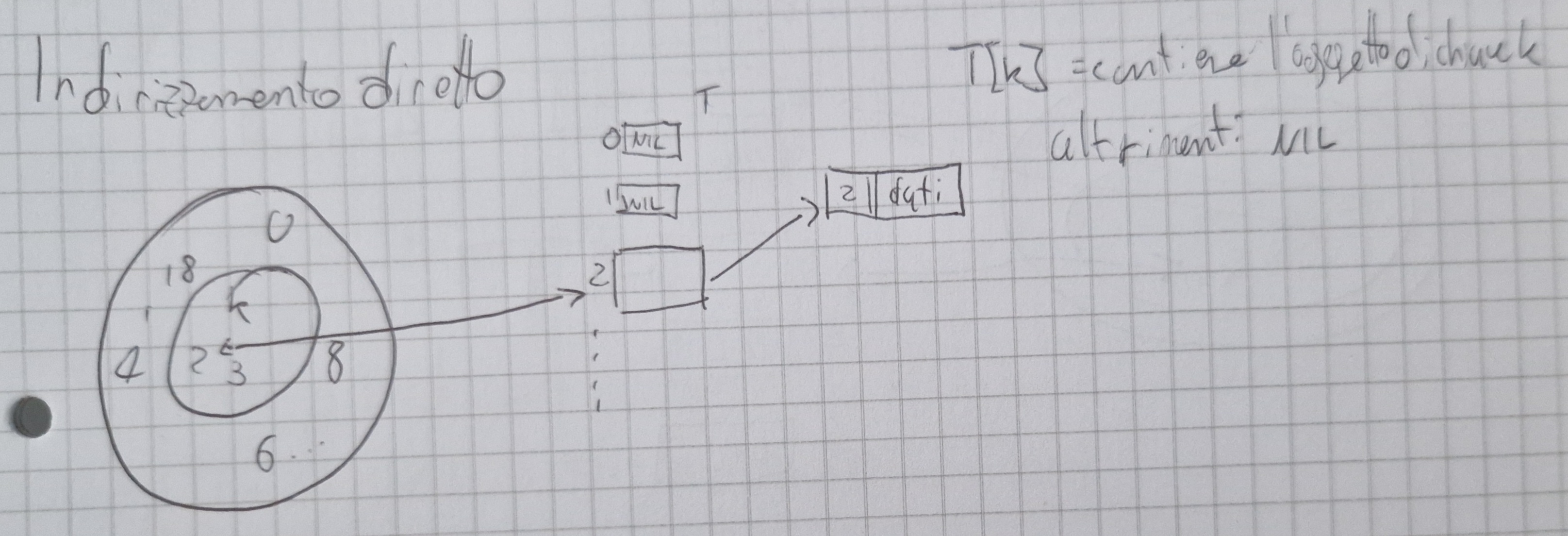
Tabelle Hash
Una tabella hash usa una memoria proporzionale al numero di chiavi effettivamente memorizzate nel dizionario.
Idea fondamentale: oggetto di chiave k è memorizzato in una cella di indice h(k), dove h è una funzione hash.
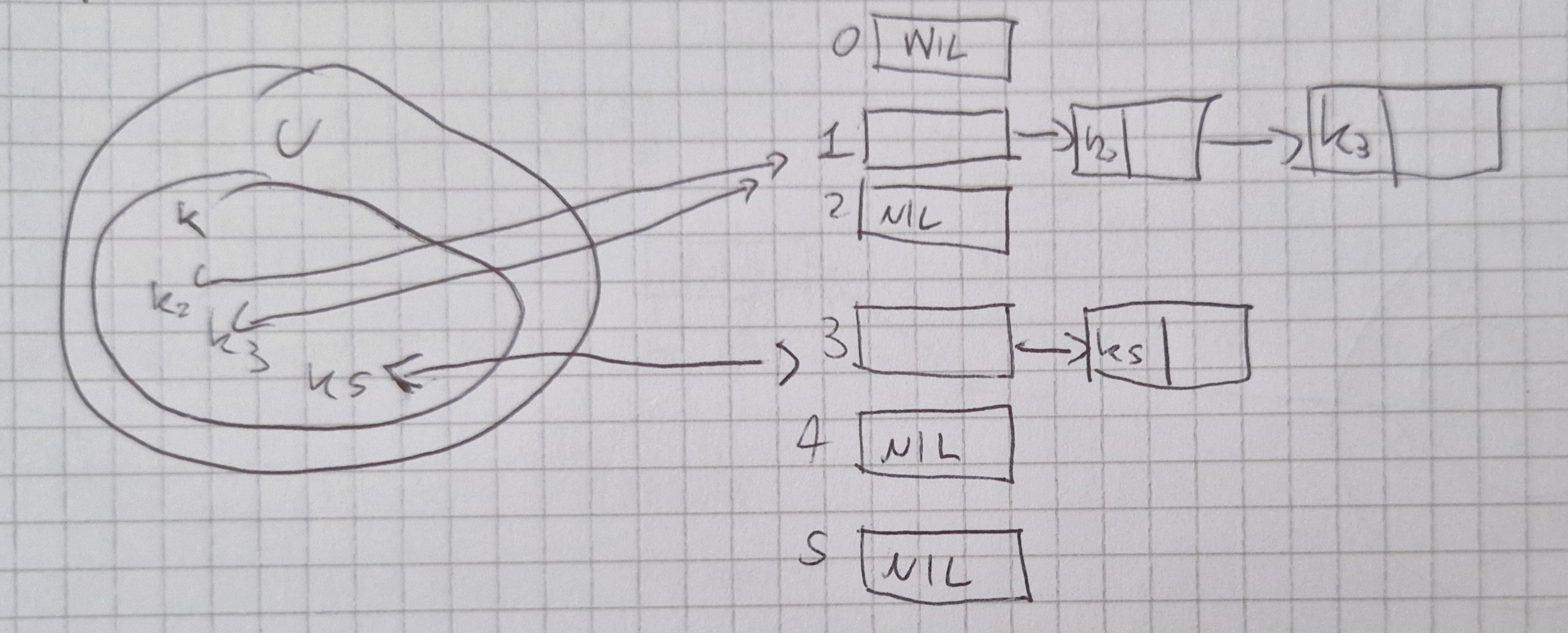
Collisioni
Problema: ho |U| possibili chiavi ed una funzione che le deve mappare su un numero m < |U| di slot o bucket della tabella
- Avrò delle chiavi diverse (molte) k_1, k_2 tali che h(k_1)=h(k_2)
- Ho collisioni
Una possibile soluzione è il concatenamento (chaining)
Operazioni:
- INSERT
- SEARCH
- DELETE
Analisi complessità
Nel caso pessimo, tutti gli n elementi vengono memorizzati nello stesso slot quindi la complessità è quella di cercare in una lista di n elementi, cioè \Omicron(n)
- In media non accade
Siano:
- m la dimensione della tabella
- \alpha il fattore di carico, \alpha= n/m
siccome 0 \le n \le |U| avremo 0 \le \alpha \le |U|/m
Ipotesi dell’hashing uniforme semplice
Ogni chiave ha 1/m probabilità di finire in qualsiasi delle m celle di T, la lunghezza media di una lista è:
E[n_j]=\frac{1}{m} \Sigma_{i=1}^m n_i = \frac{n}{m} = \alpha
Il tempo medio per cercare una chiave k NON presente è \Theta (1+\alpha) (\Omicron (1) tempo per calcolare h(k))
\Theta (1+\alpha) è il tempo anche per trovare una chiave k presente.
\Omicron (1) per le operazioni (INSERT, etc.)
Funzioni Hash
Come si sceglie bene una funzione h ?
Ne dovrei prendere una che soddisfa l’ipotesi di hashing uniforme semplice, per farlo devo sapere la distribuzione di probabilità (NON ANCHE QUIIIIIIII :( ) delle chiavi da inserire.
Assunzione: la chiave k è un intero non-negativo.
Metodo di divisione
h(k) = k\ mod\ m
Ovvero prendo solo il resto della divisione.
Facile da realizzare e veloce
Evitare valori di m come:
- potenze di 2
di solito ad m si assegna un numero primo lontano da una potenza di 2.
Esempio
h(k) = k\ mod\ m \\ m=5 \\ Inseriamo:\ 38,12,18 \\ \frac{38}{5}=3\ hash(38)= 3 \\ si\ ha\ h(38)=3, h(12)=2, h(18)=3 \\ T=[NIL,NIL,lista(12),lista(18,38),NIL]
Metodo di moltiplicazione
Moltiplichiamo k per una costante A reale tale che 0 < A < 1, quindi prendiamo solo la parte ffrazionaria di kA, lo moltiplichiamo per m e prendiamo la parte intera.
cioè h(k)=\lfloor m(kA\ mod\ 1)\rfloor di cui x\ mod\ 1 = x - \lfloor x \rfloor è la parte frazionaria di x.
m può essere valore di A
È meglio prendere un valore di A che sia della forma s/2^w con w dimensione della parola di memoria del calcolatore.
Un valore di A proposto (da Knuth) è:
A=(\sqrt{5}-1)/2
Inveso sezione aurea
Esempio
h(k)=\lfloor m(kA\ mod\ 1)\rfloor \\ A=(\sqrt{5}-1)/2 \\ m=5 \\ 38,18,12 \\ \lfloor 38*A \rfloor =0,484 \\ \lfloor m*(38*A) \rfloor=2 \\ h(38)=2,h(12)=2,h(18)=0 \\ T=[lista(18),NIL,lista(12,38),NIL,NIL]
Indirizzamento aperto
Altro metodo per evitare collisioni
La tabella contiene tutte le chiavi, senza memoria aggiuntiva.
L’idea è quella di calcolare lo slot in cui va memorizzato l’oggetto.
h ora diventa:
h:U \times \{0,1,...,m-1\} \to \{0,1,...,m-1\}
la sequenza di ispezione deve essere una permutazione \lang 0,...,m-1 \rang
Analisi di complessità indirizzamento aperto
Ricordiamo che è necessario fare una permutazione m! per ogni \lang 0,...,m-1 \rang.
L’analisi viene fatta con fattore \alpha = n/m,n\le m,0 \le \alpha \le 1
Il numero medio di ispezioni necessarie per effettuare l’inserimento del nuovo oggetto nella tabella è m se \alpha=1, e non più di \frac{1}{(1-\alpha)} se \alpha < 1
Numero medio ispezioni per trovare un elemento presente è (m+1)/2 se \alpha =1, non più di \frac{1}{\alpha} *log(1/(1-\alpha)) se \alpha<1
Tre tecniche di ispezione
- ispezione lineare
- ispezione quadratica
- doppia hashing
Queste tre tecniche fanno uso di una funzione hash ausiliara
h':U \to \{0,1,...,m-1\}
Ispezione lineare
h(k,i)=(h'(k)+i)\ mod\ m
si parte da h'(k) e poi h'(k)+1, fino a m-1
genera solo m sequenze di ispezioni distinte.
Soffre del fenomeno dell’addensamento(clustering) primario - lunghe celle occupate consecutivamente che aumentano il tempo medio di ricerca
Esempio h(k,i)=(h'(k)+i)\ mod\ m \\ m=5 \\ h'(k)=k\ mod\ m \\ 38,12,18 \\ h(38,0)=3, h(12,0)=2, h(18,0)=3\ occupato!! \\ allora\ h(18,1)=4 \\ T=[NIL, NIL, 12, 38, 18] \\ Cancelliamo\ 38 : T=[NIL,NIL,12,DEL,18] \\ Inseriamo\ 43\ h(43,0)=3 \to T=[NIL,NIL,12,43,18]
Ispezione quadratica
h(k,i)=(h'(k)+c_1i+c_2i^2)\ mod\ m
- c_1 e c_2 costanti ausiliarie (c_2 \not ={0})
- c_1 e c_2 scelti in modo che si percorra tutta la tabella
- come prima m sequenze di ispezione distinte
- Soffre dell’addensamento secondario
- chiavi con stessa posizione iniziale danno luogo alla stessa sequenza di ispezione
Hashing doppio
h(k,i)=(h_1(k)+ih_2(k))\ mod\ m
- h_1 e h_2 sono funzioni hash ausiliarie \to h_2 deve essere primo rispetto a m
- numero di sequenza generate ora è \Theta (n^2) in quanto ogni coppia (h_1(k), h_2(k)) produce una sequenza di ispezione distinta.
Alberi e grafi
Alberi Binari
Gli alberi binari si rappresentano mediante strutture dati concatenate, ogni noda ha:
- key, chiave del nodo.
- p, puntatore al nodo padre.
- left, puntatore al sottoalbero sinistro.
- right, puntatore al sottoalbero destro.
Ogni albero T ha un attributo, T.root, che è il puntatore alla radice dell’albero.
x.p=NIL sse è la radice.
s.left=NIL se sottoalbero sinistro del nodo è vuoto.
s.right=NIL se è quello destro.
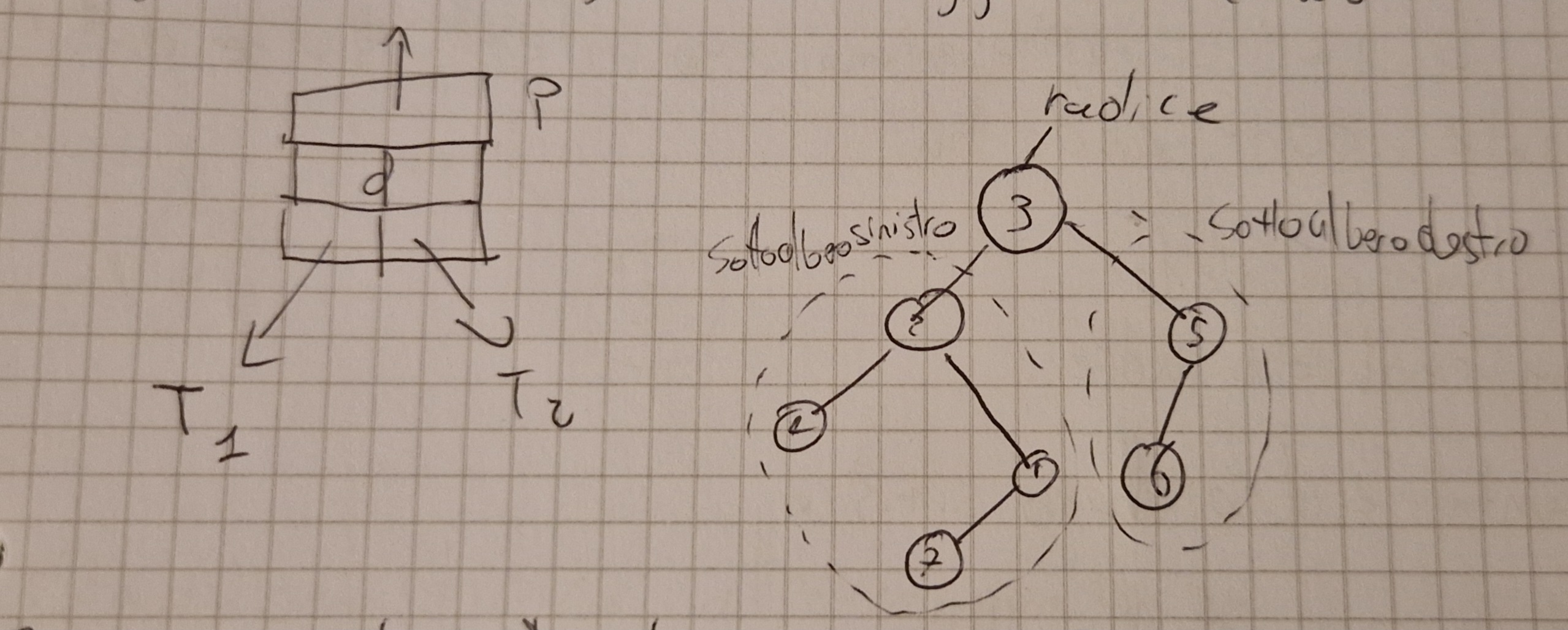
Ogni padre ha al massimo 2 figli.
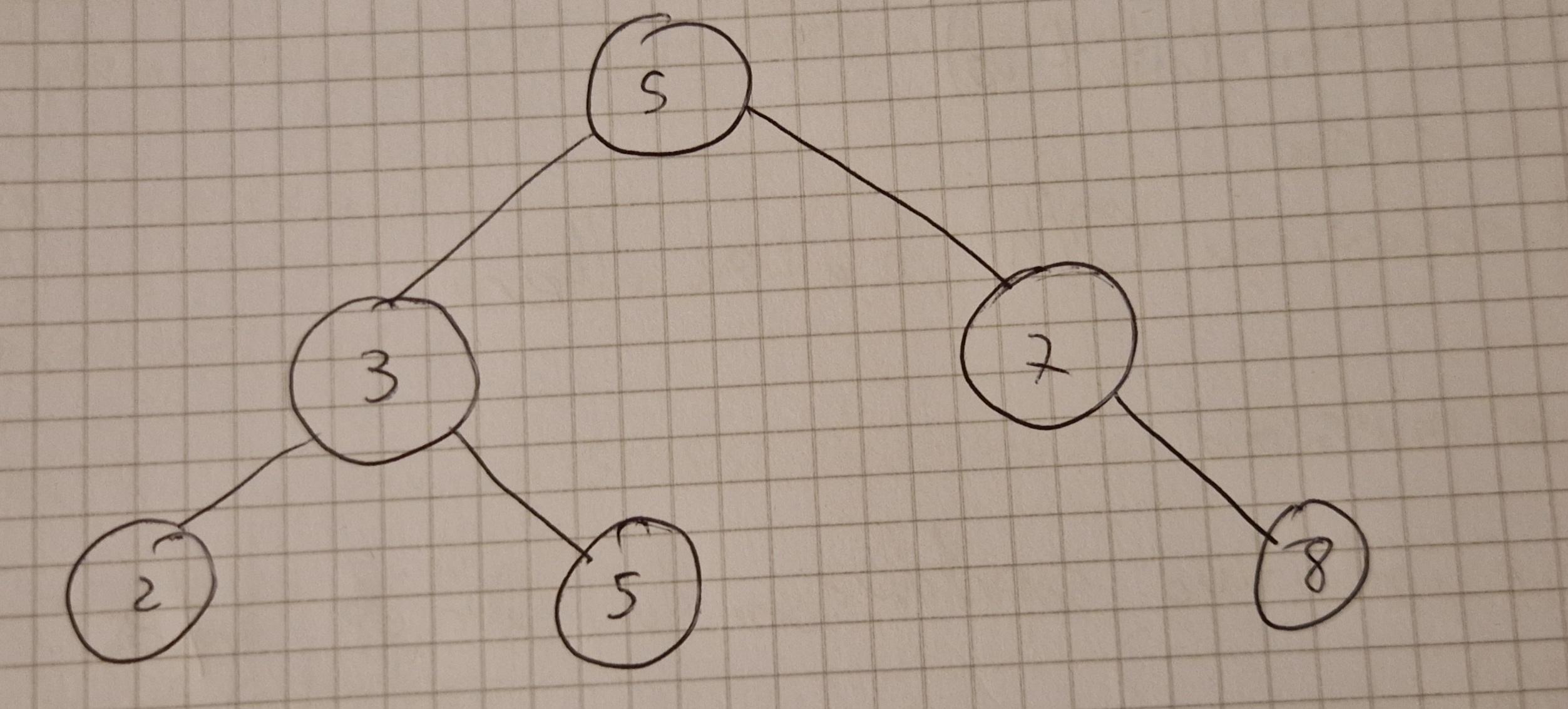
Binary Search Tree
È un albero che soddisfa la seguente proprietà:
per tutti i nodi x del BST, se l è un nodo nel sottoalbero sinistro, allora l.key \le x.key, se r è un nodo del sottoalbero destro, allora x.key \le r.key
Operazione tipica: attraversamento(walk through)
Scopo: produrre gli elementi dell’albero.
Attraversamento simmetrico (inorder tree walk):
- prima sinistro e si retsituisce
- poi radice e si restituisce
- poi destro e si restituisce
Algoritmo ricorsivo
Altre stratege di attraversamento
- Anticipato (preorder tree walk), prima radice e poi sottoalberi come prima
- Posticipato (postorder tree walk), prima sottoalberi come prima e per ultima la radice.
Operazioni sui BST
Ricerca (algoritmo intuitivo)
Tempo di esecuzione \Omicron(h), h altezza albero.
Massimo e minimo
Anche qui è intuitivo soprattutto se si ricorda la priprietà del BST.
Tempo \Omicron(h)
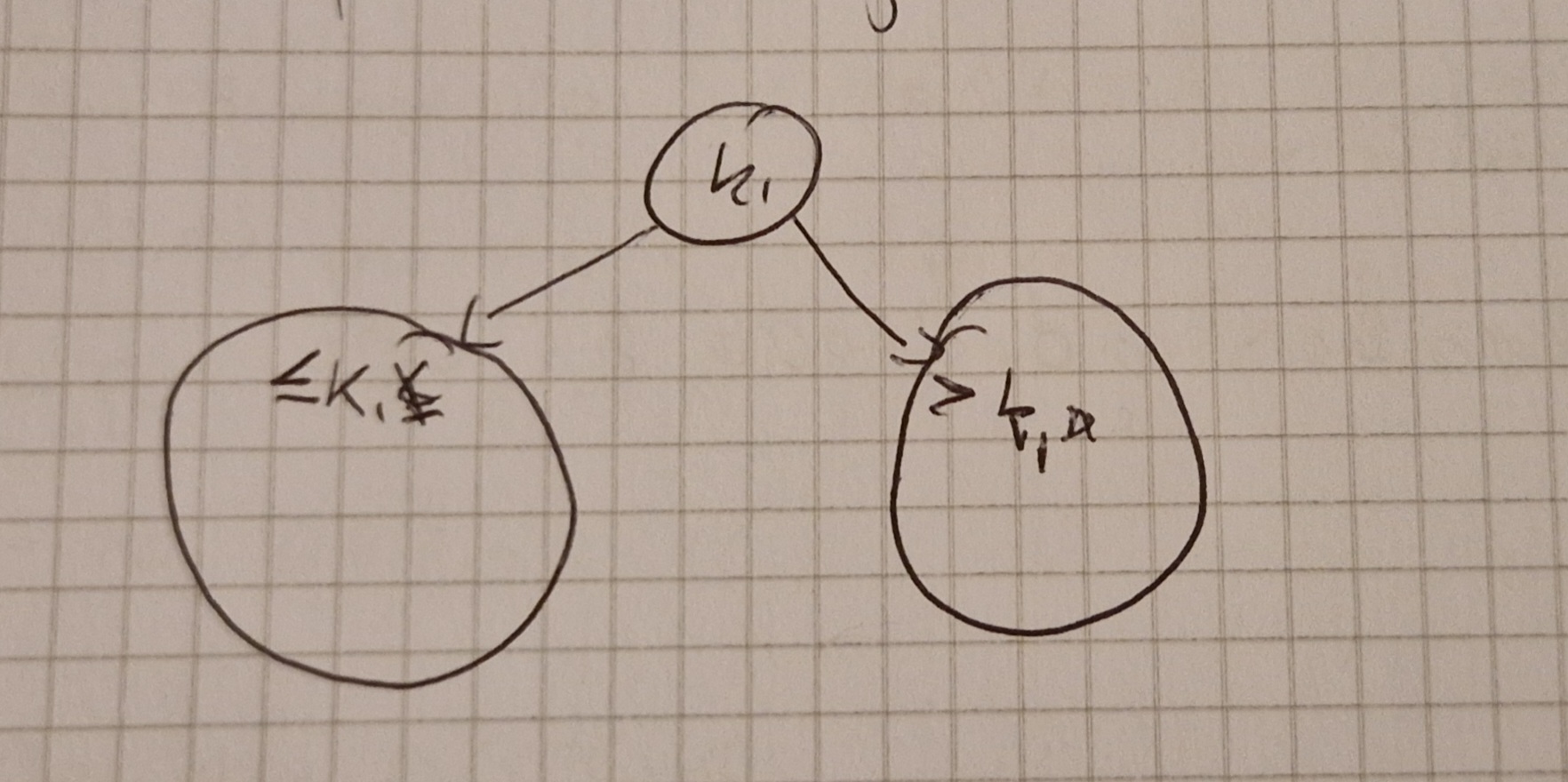
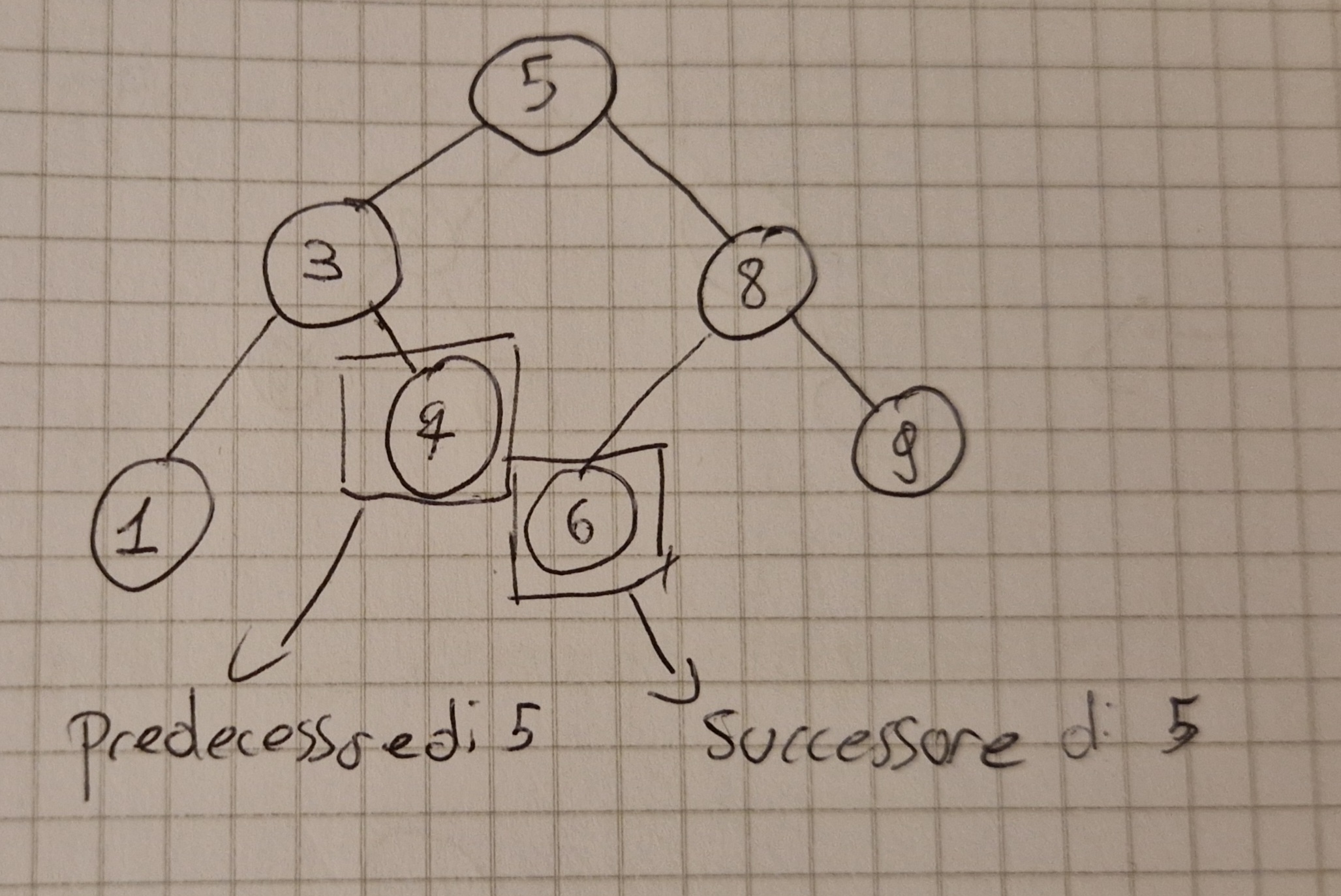
Successore e Predecessore
Il successore (predecessore) di un oggetto x in un BST è l’elemento y del BST tale che y.key è la più piccola (grande) tra le chiavi che sono più grandi (piccole) di x.key.
Tempo \Omicron(h)
Inserimento
Idea banale con confronto si trova il posto dell’elemento e si inserisce.
Cancellazione
Idea banale ma con 3 casistiche ovvero l’elemneto z da cancellare:
- non ha sottoalberi
- ha 1 sottoalbero
- ha 2 sottoalberi
Primo caso semplice si mette a NIL il puntatore del padre.
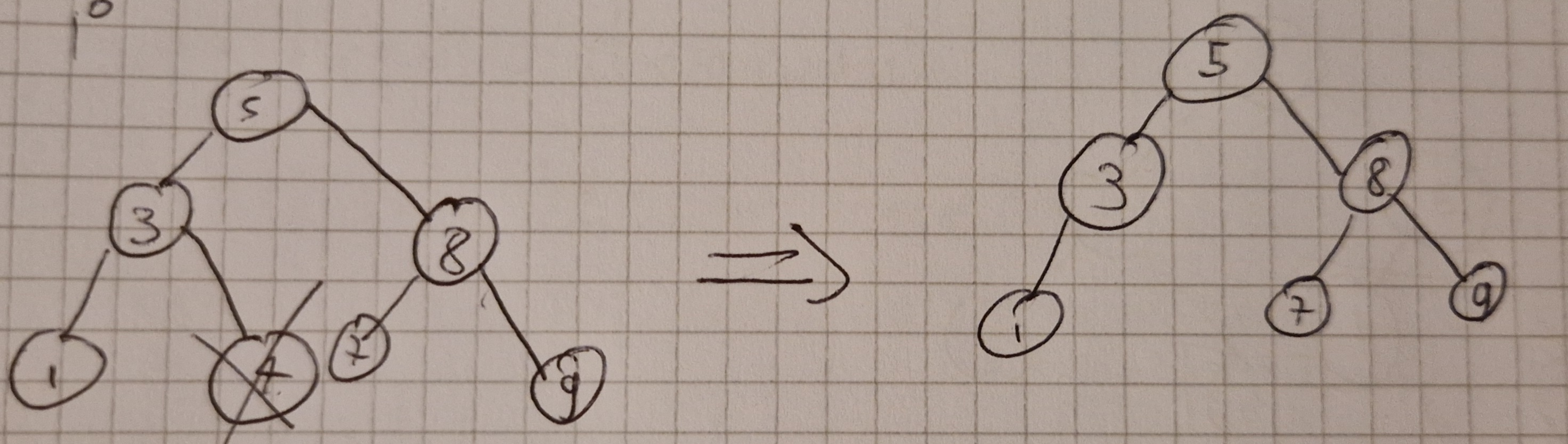
Secondo caso si sposta tutto il sottoalbero all’insù di un livello.
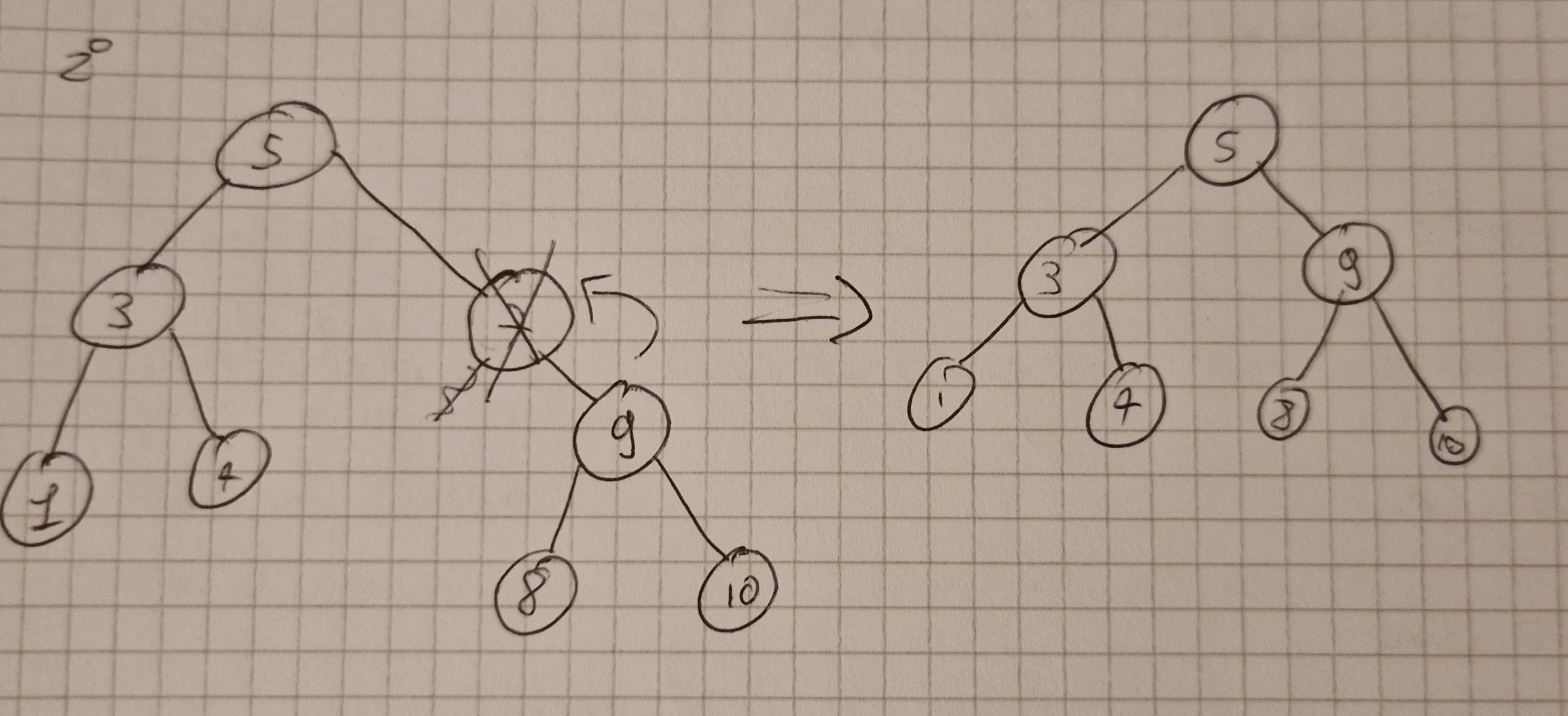
Terzo caso si trova il successore dell’elemento da cancellare e si sostituisce con l’elemento cancellato spostando il sottoalbero.
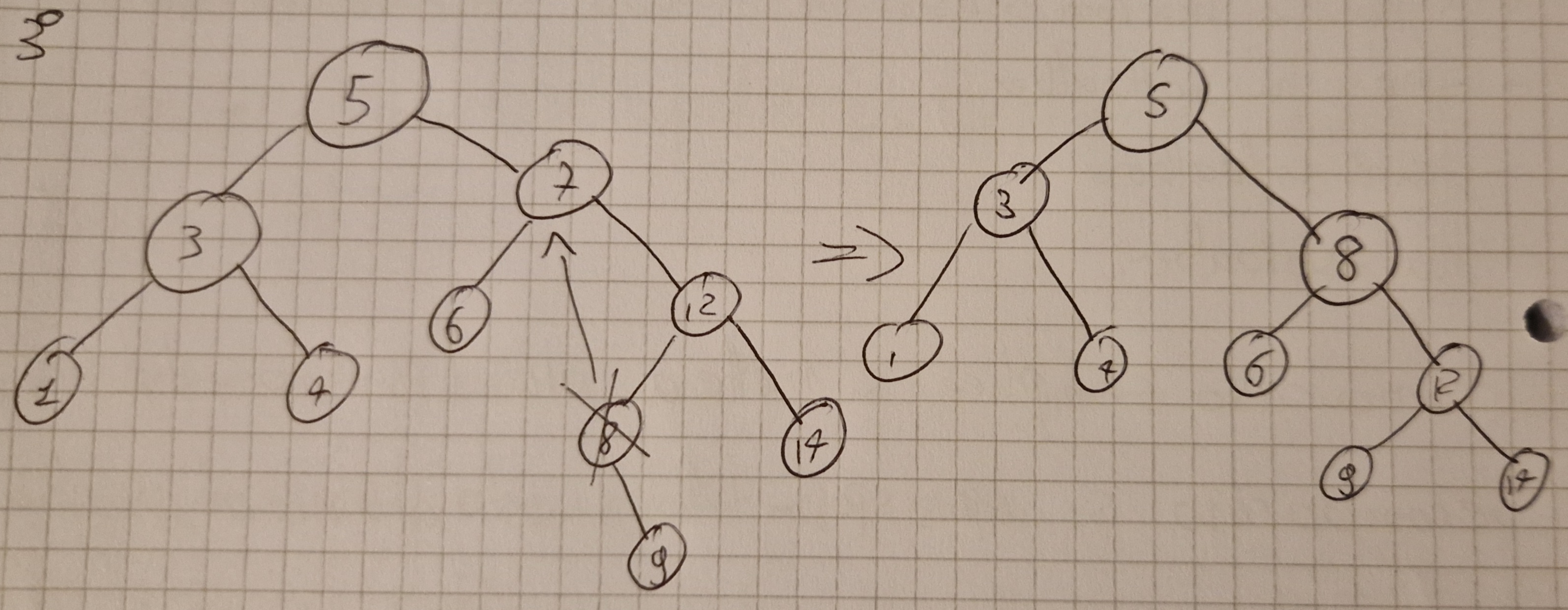
Tempo \Omicron(h)
Tutte le operazioni sui BST hanno tempo \Omicron (h)
Altezza BST
Per un albero completo h=\Theta (log(n))
Caso pessimo (in linea), h=\Theta(n)
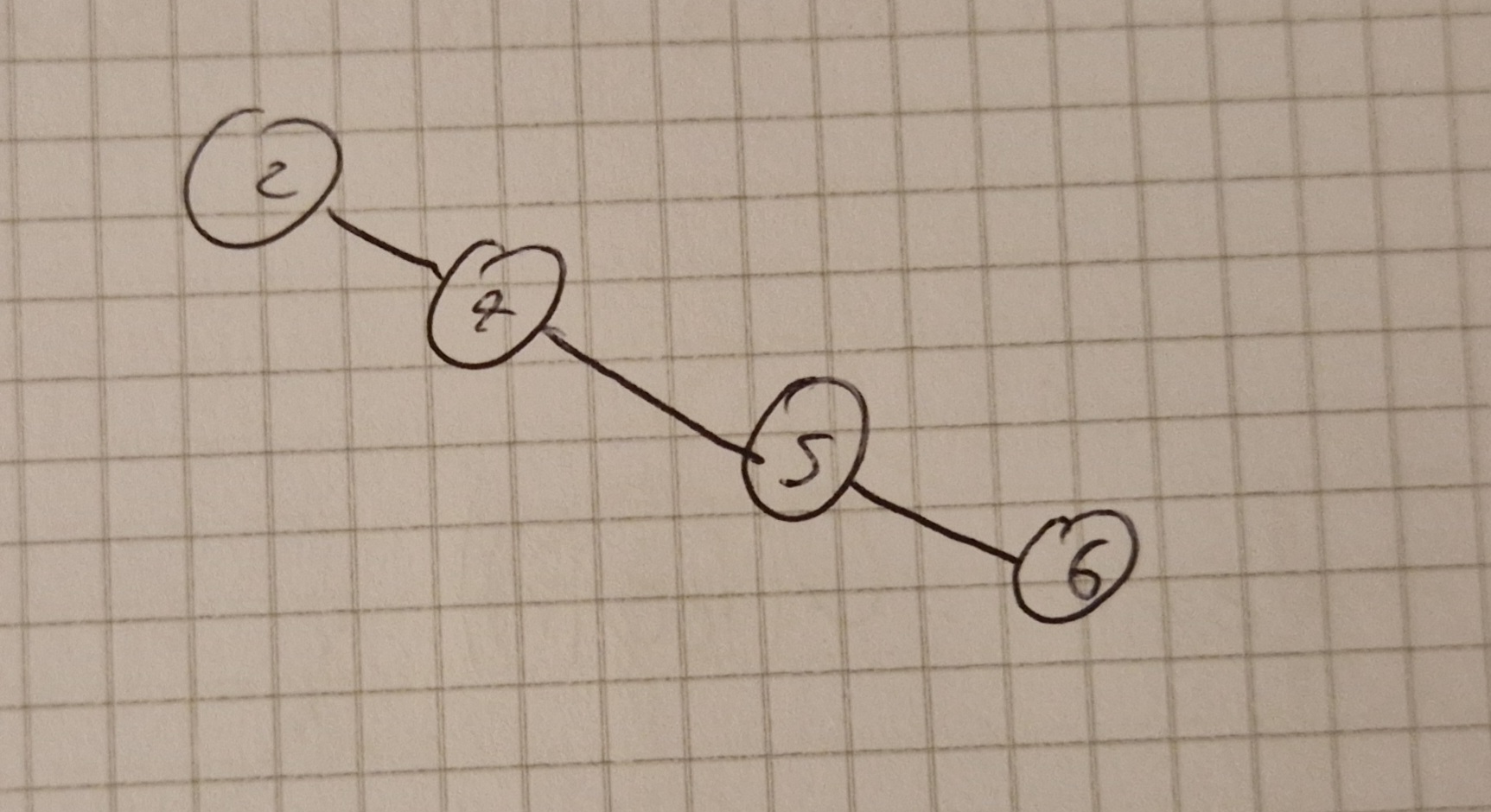
Alberi bilanciati
\Theta (log(n)) anche nel caso di alberi bilanciati.
Un albero è bilanciato sse non ci sono 2 foglie nell’albero tali che una è “molto più lontana” dalla radice, banalmente devono essere alla stessa altezza o al massimo avere una differenza di altezza di 1.
Diverse tecniche per mantenere un albero bilanciato:
- alberi rosso-neri (red-black)
- alberi AVL (Adelson-Velskii e Landis)
- Altri
L’altezza attesa di un albero costruito inserendo le chiavi in ordine casuale con distribuzione uniforme è \Omicron(log(n))
Alberi R-B
Altezza \Omicron (log(n))
Operazioni più importanti in tempo \Omicron(log(n))
È un albero bilanciato.
Idea:
- Ogni nodo ha un colore, rosso o nero.
- Colori distribuiti in modo che non si superi una differenza di altezza pari a 2.
Ogni nodo ha 5 attributi:
- key
- left
- right
- p
- color
Un BST è un RB se soddisfa queste 5 proprietà:
- Ogni nodo è o nero o rosso.
- La radice è nera.
- Le foglie (NIL) sono tutte nere
- I figli di un nodo rosso sono entrambi neri.
- Per ogni nodo x tutti i cammini da
x alle foglie sue discendenti
contengono lo stesso numero bh(x) di
nodi neri.
- bh (black height)
- il nodo x non è contato
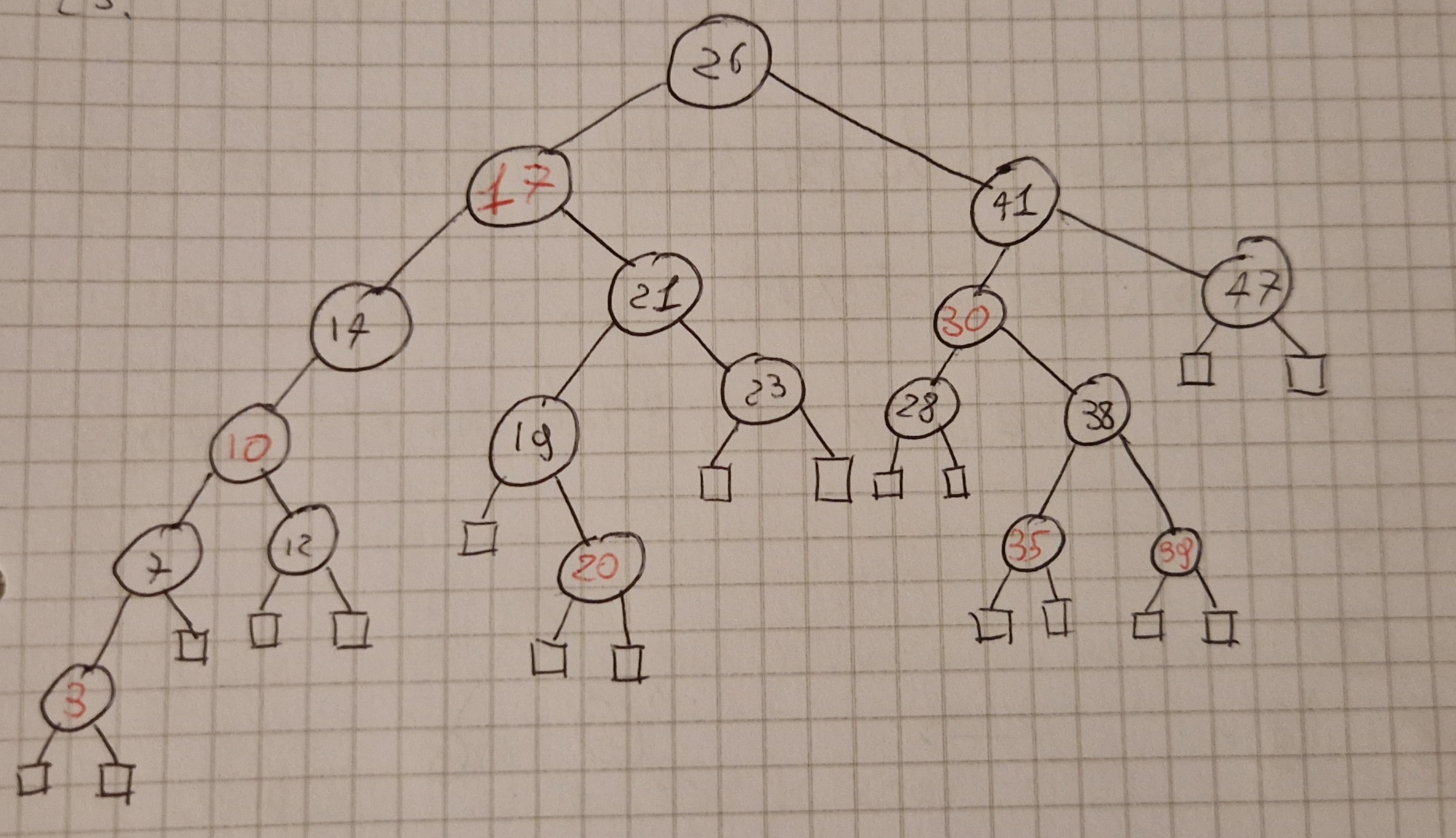
Un albero RB con n nodi interni ha altezza h \le 2log_2(n+1).
Il numero di nodi interni di un sottoalbero con radice x è \ge 2^{bh(x)}-1.
Per la 4^a priprietà almeno metà dei nodi dalla radice x ad una foglia sono neri, quindi bh(x) \ge h/2, e n \ge 2^{h/2}-1, da cui si discende h \le 2log_2(n+1)
Come conseguenza le operazioni richiedono tempo \Omicron(log(n))
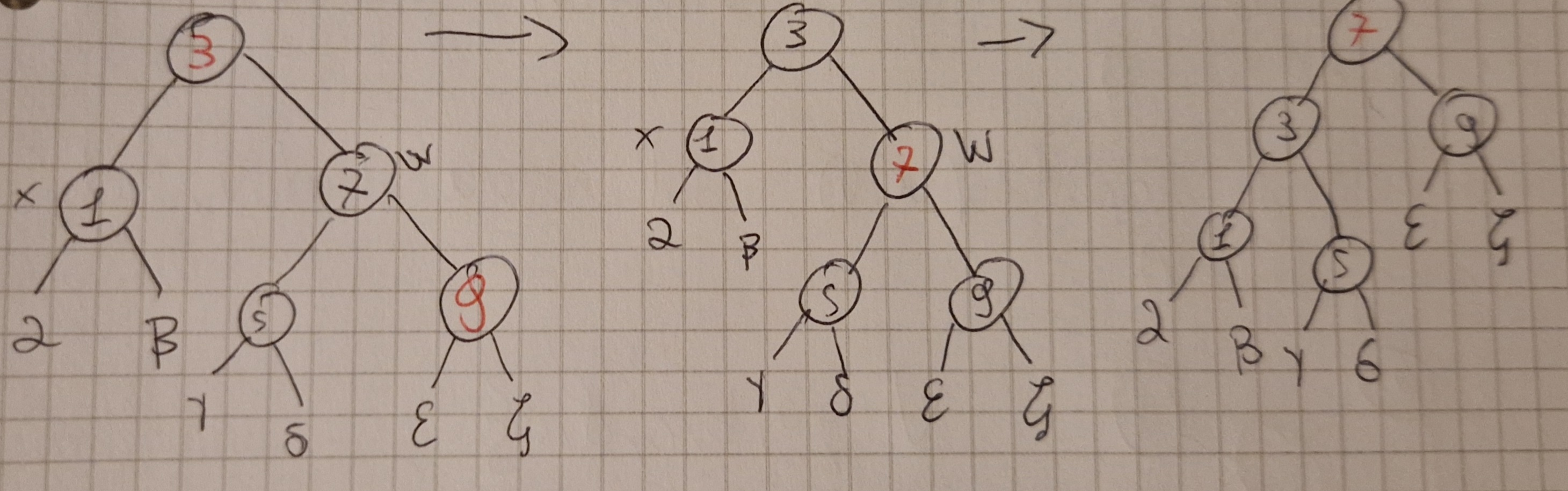
INSERT e DELETE funzionano come prima ma con una modifica per mantenere la 5^a proprietà, ovvero una rotazione a destra (RIGHT-ROTATE) o sinistra (LEFT-ROTATE)
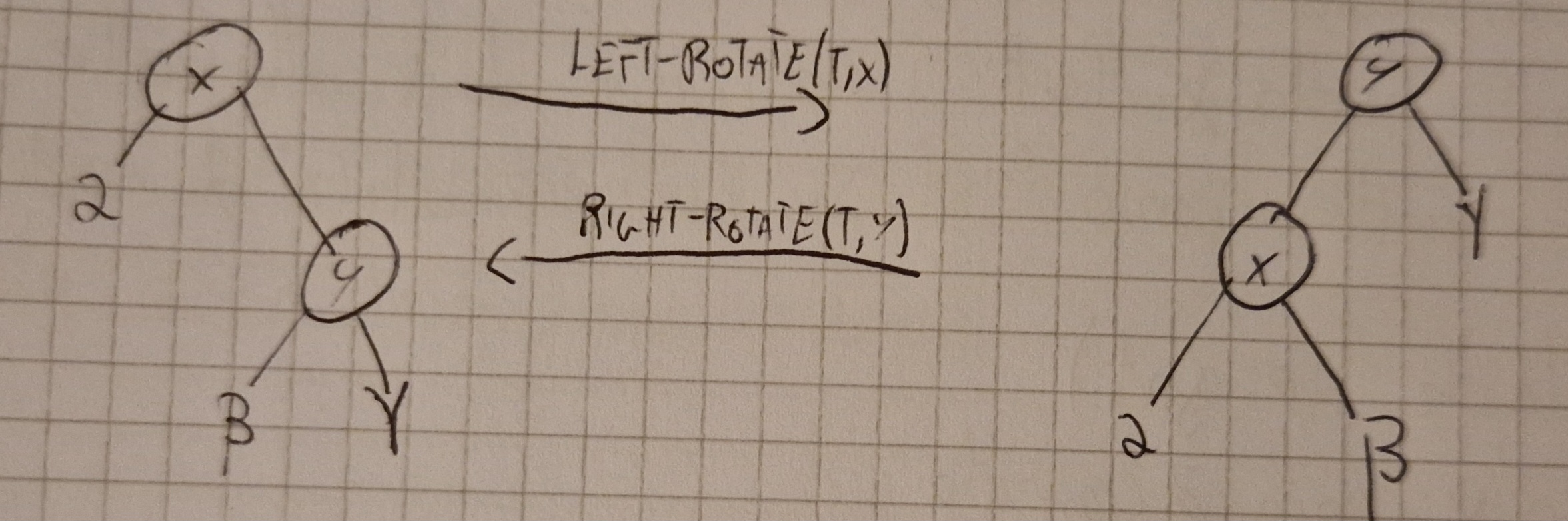
Inserimento
Uguale a BST ma ruotando per ristabilire le proprietà se necessario, si chiama INSERT-FIXUP.
RB-INSERT-FIXUP sempre su un nodo z tale che z.color=RED.
L’inserimento può dare vita ha 3 casistiche:
Primo caso: y rosso
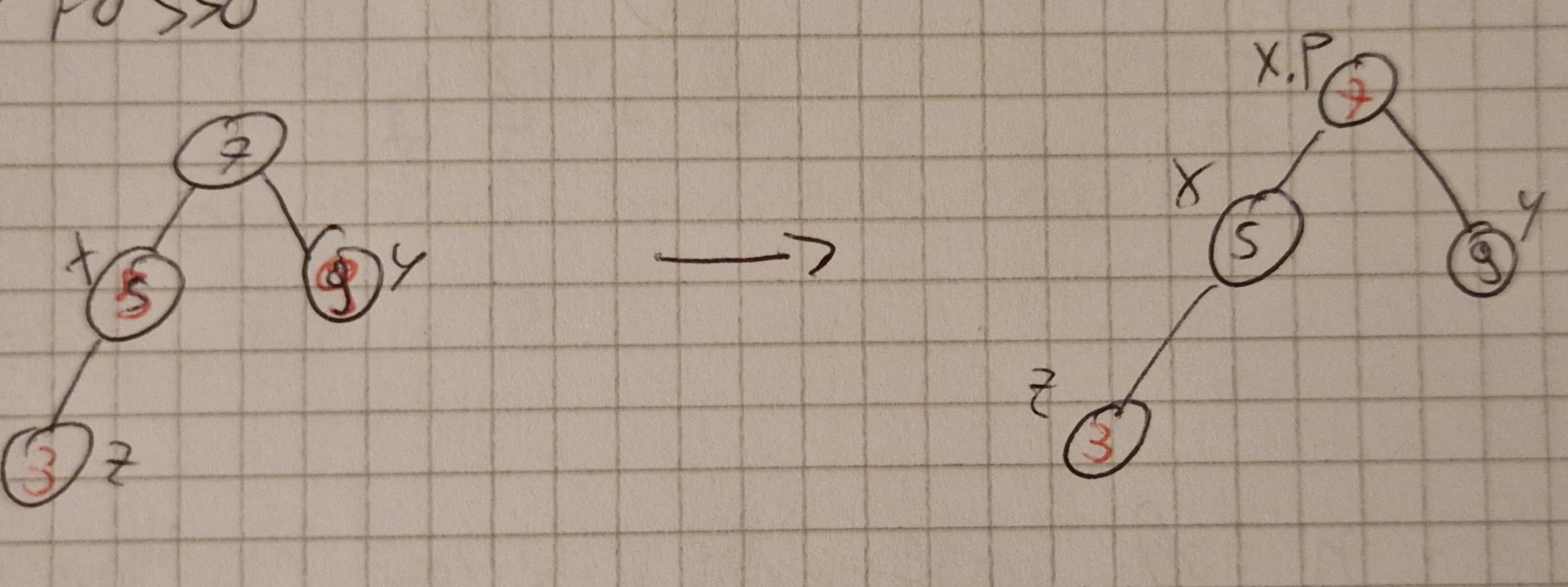
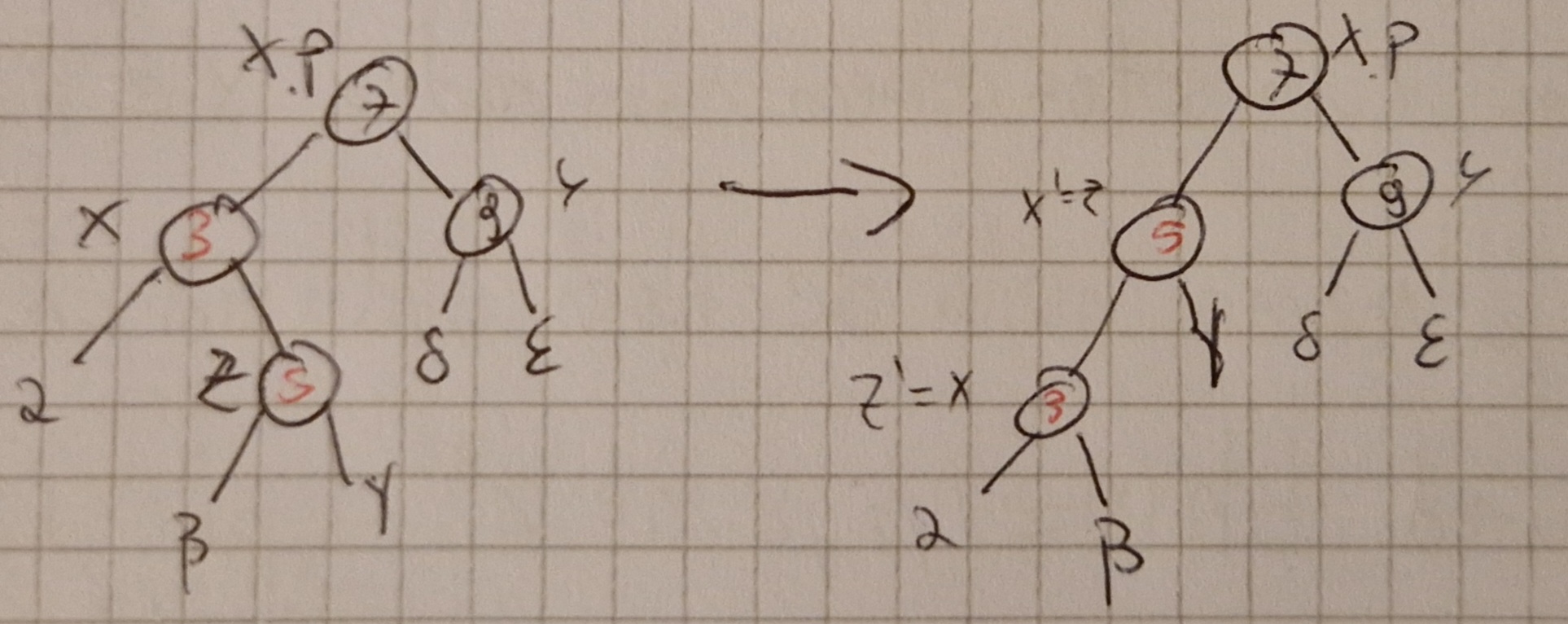
Secondo caso: y nero e z figlio destro di x
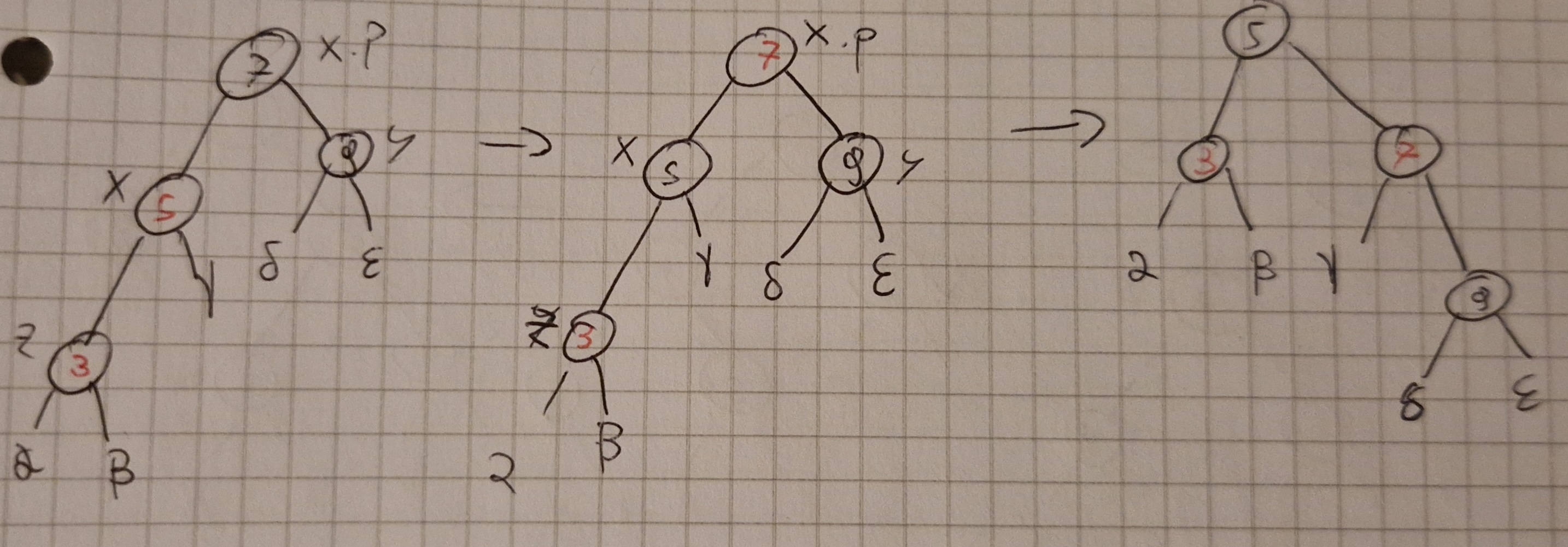
Terzo caso: y nero e z figlio sinistro di x
Può essere invocato \Omicron(h) volte, cioè \Omicron(log(n))
Funzionamento di RB-DELETE
Uguale al DELETE ma con T.nil al posto di NIL.
Se viene cancellato un nodo rosso non c’è problema.
Per com’è fatto viene eliminato un nodo (y) con al più un figlio diverso da T.nil, e se y.color=RED il nodo x che prende il posto di y è perforza nero.
Se invece y è nero si può aver violato delle proprietà:
- 1(radice rossa, se y è la radice e x è rosso)
- 3(due rossi consecutivi se y.p e x sono rossi)
- 5 (i cammini con y hanno un nero in meno)
5 casistiche:
Caso 0: x è un nodo rosso, oppure è la radice (ricordo che viene eliminato y)
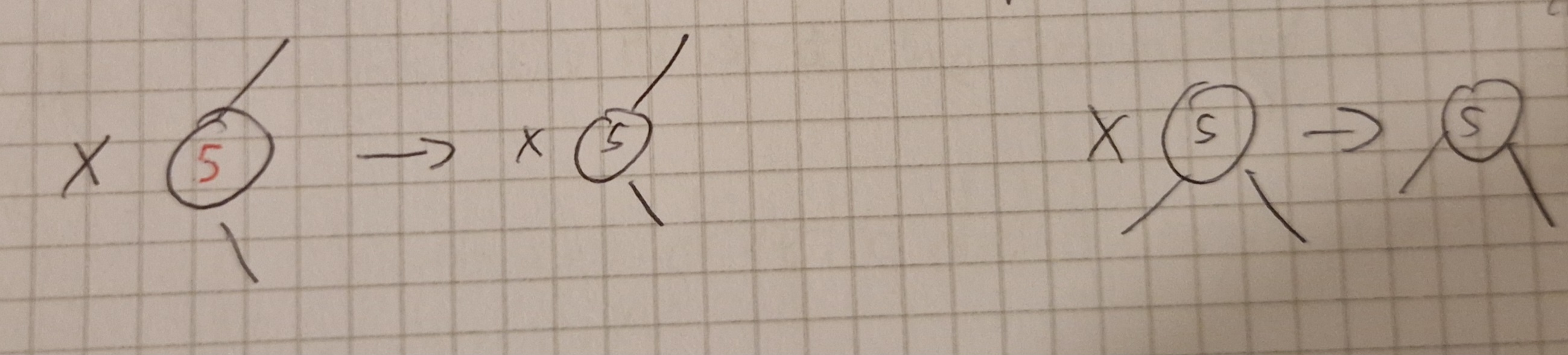
Caso 1: x è un nodo nero, il suo fratello destro w è rosso, e di conseguenza il padre x.p è nero.
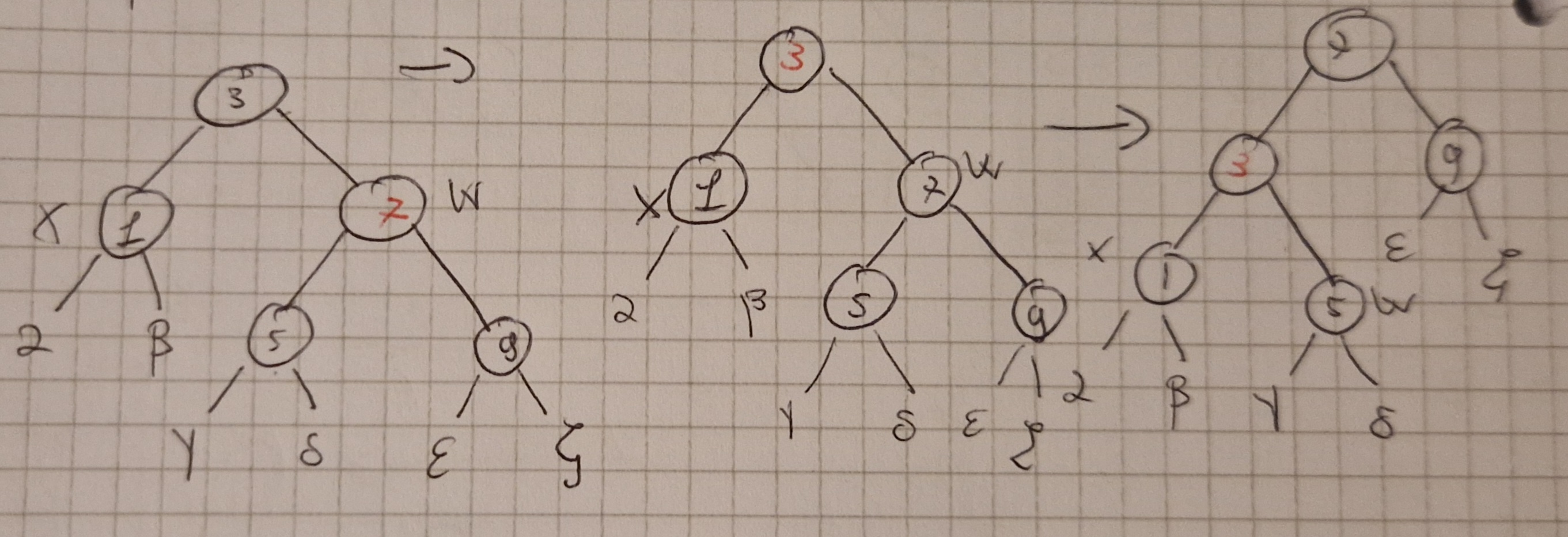
Caso 2: x è nero, suo fraltello destro è nero con figli entrambi neri.
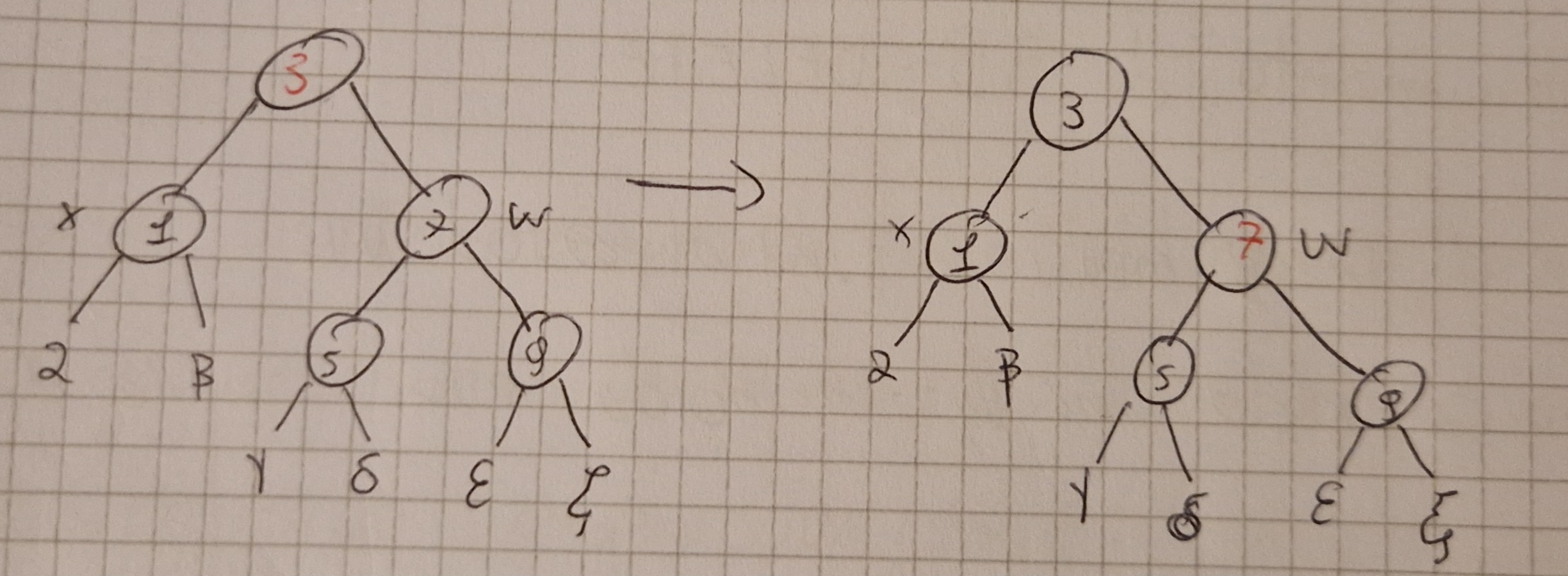
Caso 3: x è nero, suo fratello destro w è nero con figlio sinistro rosso e figlio destro nero.
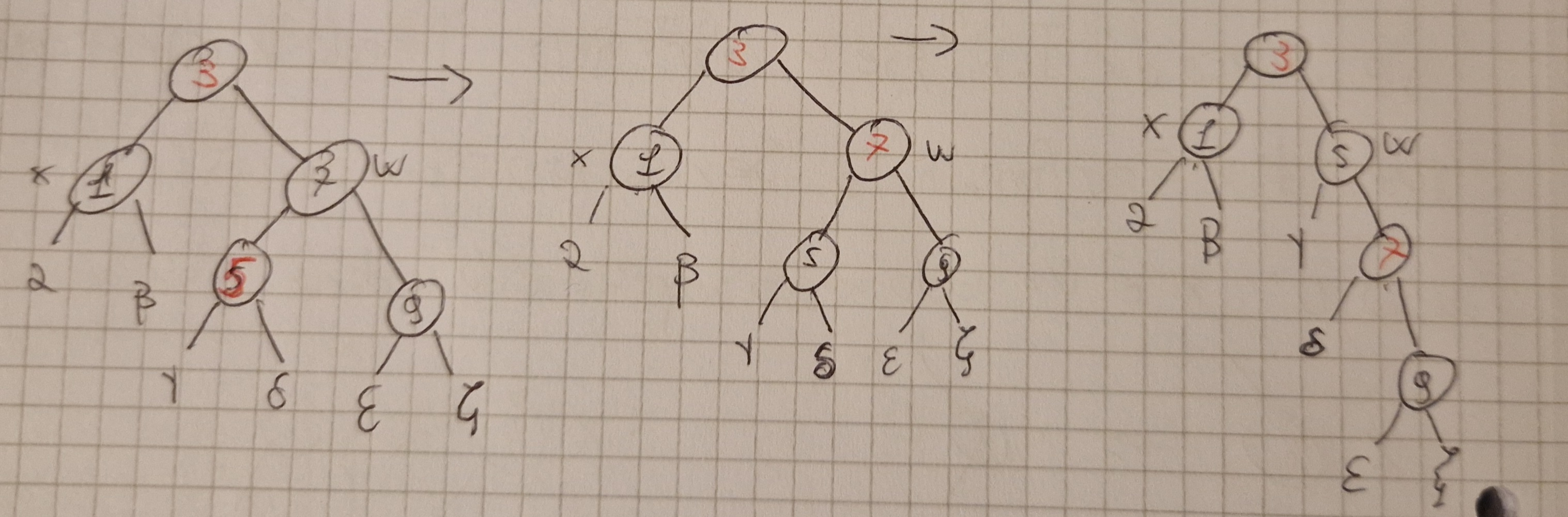
Caso 4: x è nero, suo fratello destro w è nero con figlio destro rosso.
Grafi
Richiamo ai grafi
Un grafo è una coppia G=(V,E) in cui:
- V è un insieme di nodi (detti vertici)
- E è un insieme di archi (detti anche lati, o edges)
Un arco è una connessione tra 2 vertici
- 2 vertici connessi da un arco sono detti adiacenti
- se un arco e connette 2 vertici u e v, può essere rappresentato dalla coppia (u,v) di vertici che connette, quindi E \sube V^2
- |V| è il numero di vertici del grafo, mentre |E| è il numero di archi, 0 \le |E| \le |V|^2
Ci sono 2 tipi di grafi: orientati e non orientati.
- In un grafo non orientato, un arco (u,v) è lo stesso di (v,u) (non c’è direzione)
- In un grafo orientato (u,v) “va dal” nodo u “al” nodo v, ed è diverso da (v,u).
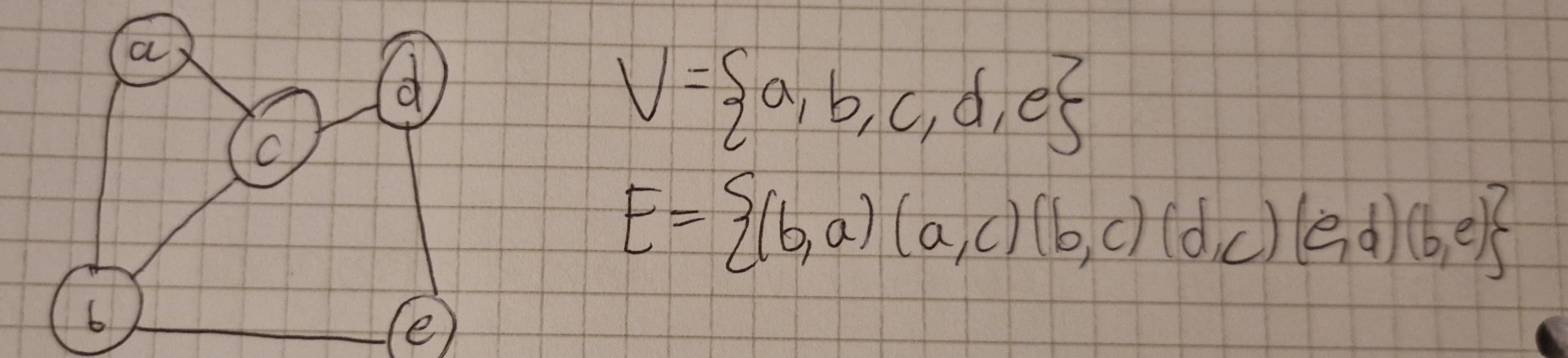
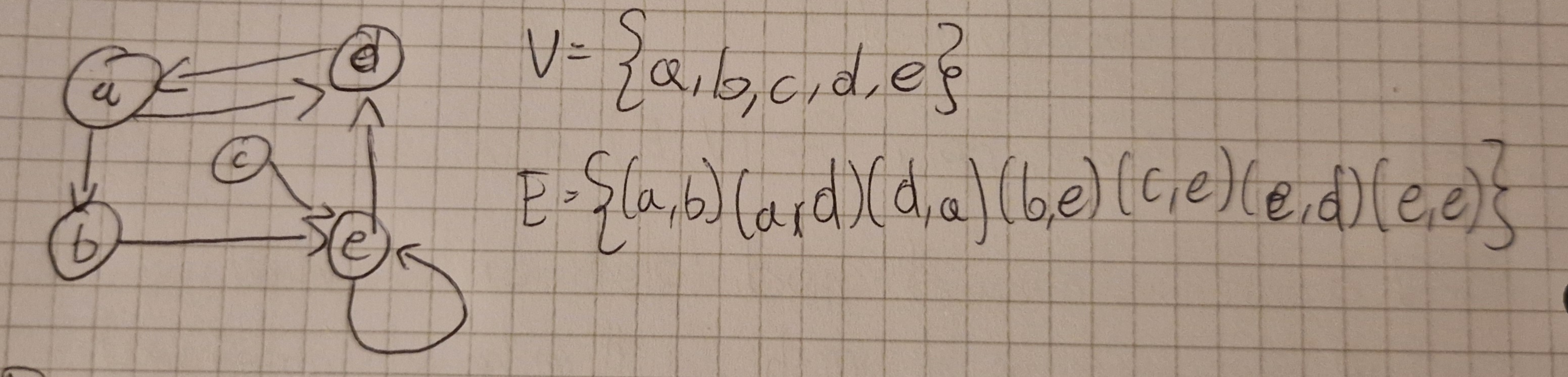
Rappresentazione di grafi in memoria
2 tecniche principali:
- liste di adiacenza
- matrice di adiacenza
graph TD;
A-->D;
A-->B;
D-->A;
B-->E;
C-->E;
E-->D;
E-->E;
DIiensione delle rappresentazioni dei grafi
Nel caso di liste di adiacenza abbaimo un array di liste:
- una lista per ogni nodo del grafo
- per ogni vertice v, la lista corrispondente contiene i vertici adiacenti a v.
Nella matrice di adiacenza M, l’elemento m_{ij} è 1 se c’è un arco dal nodo i al j, 0 altrimenti.
In entrambi i casi, dato un nodo u in un grafo G, l’attributo u.Adj rappresenta l’insieme di vertici adiacenti a u.
Liste di Adiacenza:
- Numero totale di elementi nelle liste è |E|.
- Numeri di elementi nell’array è |V|.
- Complessità spaziale \Theta (|V|+|E|)
Matrice di Adiacenza:
- La dimensione della matrice è |V|^2, complessità \Theta (|V|^2)
Liste migliori quando |E| \not ={\Theta (|V|^2)}, cioè grafo sparso, si ricorda |E| \le |V|^2 cioè |E|=\Omicron (|V|^2).
Se grafo completo (o quasi), tanto vale usare la matrice.
Un grafo è completo quando per ogni coppia di nodi u e v, sia l’arco (u,v) che l’arco (v,u) sono in E.
Rappresentazione di grafi non orientati
L’arco (u,v) non orientato come 2 archi orientati uno da u a v e uno da v a u.
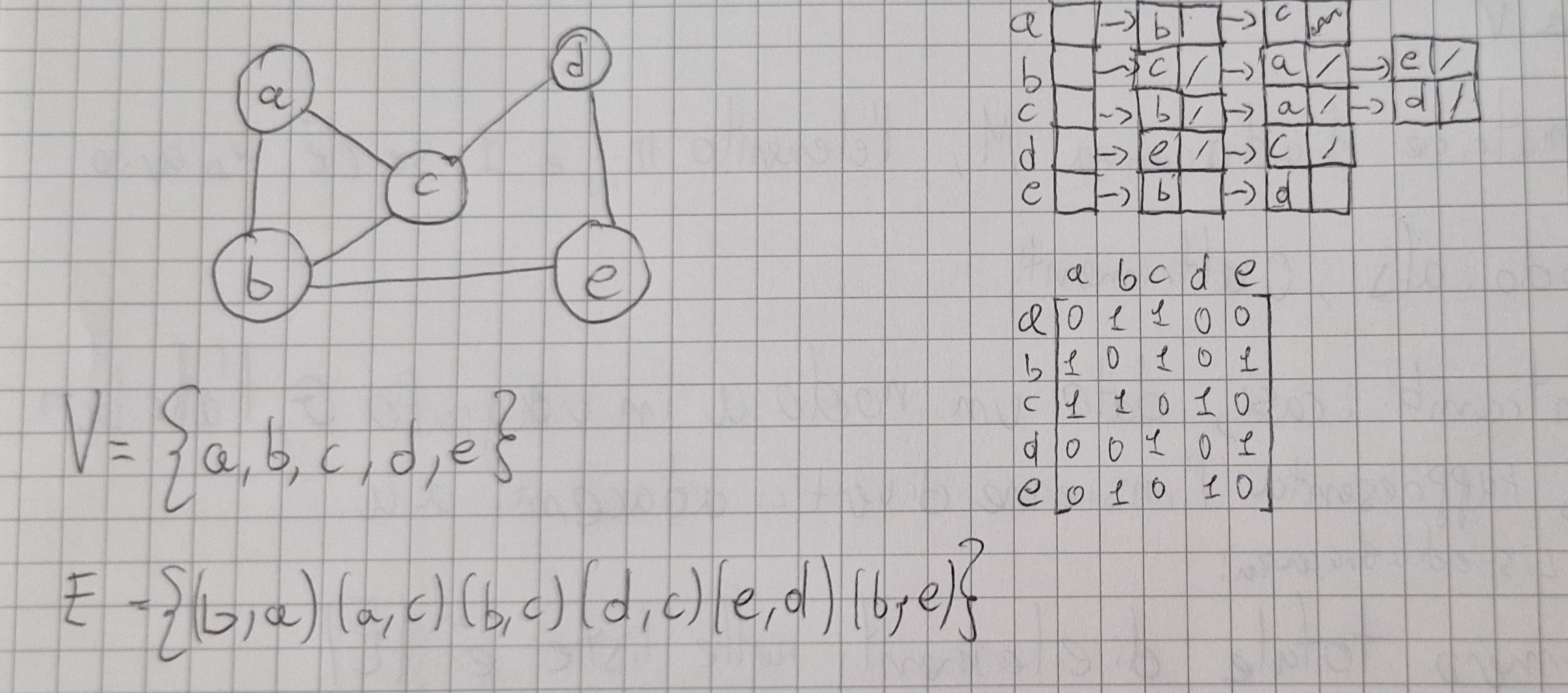
Matrice di adiacenza simmetrica, quindi basta guardare la diagonale superiore principale.
Visita in Ampiezza (Breadth-First Search)
Problema:
- input: un grafo G, e un nodo s (sorgente) di G.
- output: visitare tutti i nodi di G che sono raggiungibili da s.
Algoritmo Breadth-First Search
Idea: prima visitiamo i nodi che distano 1 da s, poi 2, poi 3, etc.
Qunado si visita un nodo, si tiene traccia della distanza da s in un attributo u.dist.
Mentre si visitano i nodi si colorano:
- bianco, NON visitato
- grigio, visitato ma dobbiamo ancora visitare i nodi adiacenti
- nero, visitato e concluso
Complessità di BFS \Omicron (|V| + |E|)
Ricerca in Profondità (Depth-First Search)
BFS politica FIFO
DFS invece LIFO
Idea: ogni volta che mettiamo un nodo in cima allo stack, si comincia subito a visitare i nodi adiacenti.
Problema risolto dall’algoritmo DFS
- input: un grafo G
- output: visitare tutti i nodi di G, con BFS si raggiungono solo i nodi raggiungibili da s
DFS usato spesso come sottoalgoritmo, stessa colorazione di BFS.
Complessità di DFS è \Theta (|V| + |E|).
Grafo Orientato Aciclico
Supponiamodi avere un grafo orientato aciclico (directed acyclic grafh, DAG) che rappresenta le precedenze tra gli eventi.
Esempio
graph TD;
Orologio;
Mutande-->Pantaloni;
Mutande-->Scarpe;
Calze-->Scarpe;
Pantaloni-->Scarpe;
Pantaloni-->Cintura;
Cintura-->Giacca;
Camicia-->Cintura;
Camicia-->Cravatta;
Cravatta-->Giacca;Ordinamento Topologico
Un ordinamento topologico di un DAG è un ordinamento lineare dei nodi del grafo tale che, se nel DAG c’è un arco (u,v), allora nodo u precede v.
Esempio con il grafo sopra:
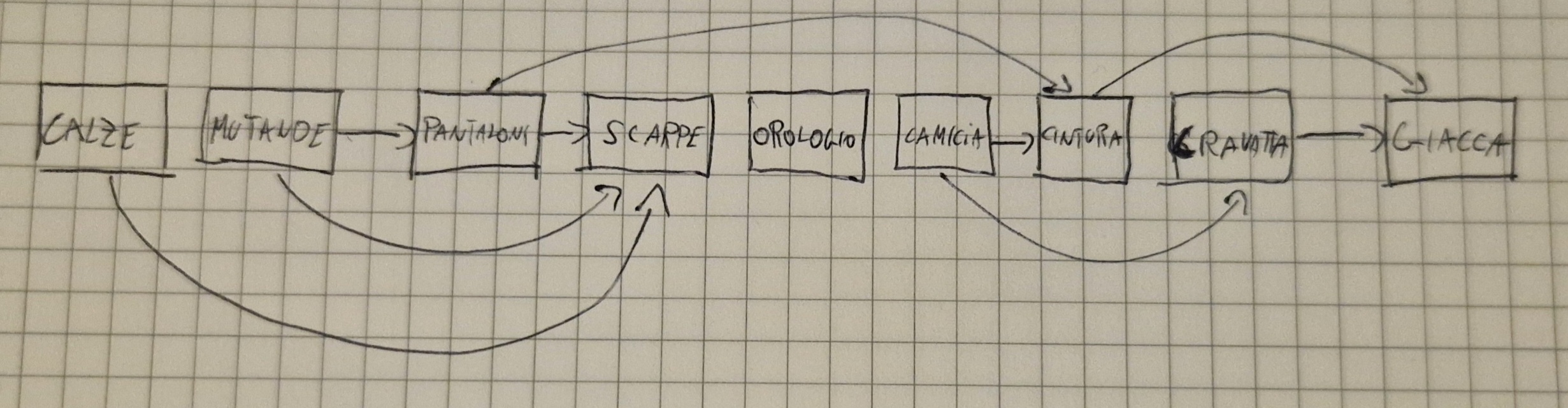
- Ordinamento topologico fornisce ordinamento che rispetta le precedenze degli eventi.
- Problema del DAG:
- input: un DAG G
- output: ordinamentto topologico di G
Idea:
- Visito DAG con algoritmo DFS.
- Quando un nodo u di G viene colorato di nero, inseriamo il nodo u in testa alla lista.
- Restituisco la lista.
Tempo: \Theta (|V|+|E|).
Argomenti Avanzati (NON presenti nell’esame)
Cammini Minimi
Si vuole avere il cammino minimo tra due nodi.
Ingresso: G=(V,E) orientato, funzione di peso W:E\to R
Peso cammino
p= \lang v_0, v_1,...,v_k\rang \\ W(p)=\Sigma_{i=1}^k w(v_{i-1},v_i)
Peso cammino minimo tra u e v:
\delta (u,v)=\begin{cases} min\{w(p):u \to^p v\}\ se\ esiste\ cammino\ p\ da\ u\ a\ v \\ \infty\ altrimenti \end{cases}
Non sono ammessi cicli negativi.
Calcoliamo i cammini minimi da nodo fissato s.
Uscita:\forall v \in V: d[v]=\delta (s,v)
- inizio d[v]=\infty
- Progressivamente ridotto, ma d[v] \ge \delta (s,v) sempre.
- d[v] stima di cammino minimo.
- Pi[v]= predecessore di v nel cammino min da s.
Programmazione dinamica
Come divide-et-impera, si scompone il problema, si risolvono i sotto-problemi e si ricompone.
Spesso usata per l’ottimizzazione.
Problema:Taglio delle aste
- Prezzo asta dipende dalla lunghezza
- Problema: date delle aste di lunghezza n che posso tagliare in pezzi più corti, trovare il modo ottimale di tagliare le aste per massimizzare il ricavo che posso derivare dalla vendita delle aste.
- Potrei vendere l’asta intera.
Esempio tabella

Se asta lunga 4 posso vederlo: [4](9);[1,3](9);[2,2](10);[3,1](9);[1,1,2](7);[1,2,1](7);[2,1,1](7);[1,1,1](4)
taglio ottimale:[2,2]
Data lunghezza n, ci sono 2^{n-1} modi di taglio.
r_n ricavo massimo.
r_4=10,r_{10}=30(venduta intera).
r_n è della forma r_i+r_{n-1}
In altre parole:
r_n=max(p_n,r_1+r_{n-1},...,r_{n-1}+r_1) \implies r_n = max_{1\le i\le n}(p_i+r_{n-i}).
Procedura ricorsiva di questa espressione ha costo temporale: T(n)=c+\Sigma_{j=0}^{n-1} T(j)
Algoritmi golosi
A volte non serve provare tutte le soluzioni basta dimostrare che sia una quella ottimale, ciò è chiamato algoritmo goloso (greedy).
In generale gli algoritmi golosi si muovono per ottimi locali (soluzioni).
Spesso in problemi difficili però l’ottimo locale rappresenta una buona approsimazione dell’ottimo globale.
n attivita a_1,a_2,...,a_n usano stessa risorsa.
Ogni a_i ha un tempo di inizio s_i ed un tempo di fine f_i con s_i <f_i.
a_i occupa la risorsa nell’intervallo temporale [s_i,f_i).
a_i e a_j compatibili se [s_i,f_i) e [s_j,f_j) disgiunti.
Esempio

Insieme di attività computabili : \{a_3, a_9, a_{11}\}.
Max numero attività computabili: 4
Esempio: \{a_2, a_4, a_9, a_{11}\}.
Definiamo s_{ij} l’insieme delle attività che iniziano dopo la fine di a_i e terminano prima dell’inizio di a_j.
A_{ij} insieme massimo attività computabili in S_{ij}.
Mettiamo in una tabella c, c[i,j]=|A_{ij}|
\implies c[i,j]=c[i,k]+c[k,j]+1.
Per risolvere il problema di ottimizzazione basta ogni volta scegliere l’attività che finisce prima, quindi ripetere l’operazione sulle attività che iniziano dopo quella scelta.
Complessità \Theta(n).
Complessità e non determinismo
Data funzione T(n), indichiamo con DTIME(T) l’insieme dei problemi tali che esiste un algorirmo che li risolve in tempo T(n).
DTIME(T) classe dei linguaggi riconducibili in tempo T mediante macchine di Turing deterministiche a k nastri di memoria, idem DSPACE(T).
NTIME(T) e NSPACE(T) uguali ma macchine Turing non deterministiche.
Fondamentale classe di problemi:
P=U_{i\ge 1} DTIME(O(n^i)), chiamati trattabili.
NP=U_{i \ge 1} NTIME(O(n^i))
P=NP? Probabilmente no, ma non si è ancora dimostrato.
\mathcal{L} classe di linguaggi, diciamo che un linguaggio L è \mathcal{L}-difficile rispetto alle riduzioni in tempo polinomiale sse, \forall L' \in \mathcal{L}, è riducibile in tempo polinomiale a L.
L è \mathcal{L}-completo se è \mathcal{L}-difficile ed è in \mathcal{L}.
Computer quantistici
Qubit può non solo trovarsi a 0 e 1, ma anche in sovrapposizione tra i due stati.
Supremazia quantistica: risolve problemi difficili molto più efficiente che con i computer classici.
I computer quantistici possono risolvere efficientemente i problemi NP-difficili? No.
Algoritmi
Qui sono presenti tutti gli algoritmi presentati in pseudo-codice





